摘要:19.向量...a为常数 (1)求关于x的函数关系式 (2)若时.的最小值为-2.求a的值 结论中函数在一个周期内的图象.
网址:http://m.1010jiajiao.com/timu3_id_4471251[举报]
已知向量
=(cos2ωx-sin2ωx,sinωx),
=(
,2cosωx),函数f(x)=
•
(x∈R)的图象关于直线x=
对称,其中ω为常数,且ω∈(0,1).
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)若将y=f(x)图象上各点的横坐标变为原来的
,再将所得图象向右平移
个单位,纵坐标不变,得到y=h(x)的图象,求y=h(x)在[-
,
]上的取值范围.
查看习题详情和答案>>
| a |
| b |
| 3 |
| a |
| b |
| π |
| 2 |
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)若将y=f(x)图象上各点的横坐标变为原来的
| 1 |
| 6 |
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
已知向量
=(cos2ωx-sin2ωx,sinωx),
=(
,2cosωx),设函数f(x)=
•
(x∈R)的图象关于直线x=
对称,其中ω为常数,且ω∈(0,1).
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)若将y=f(x)图象上各点的横坐标变为原来的
,再将所得图象向右平移
个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间[0,
]上有且只有一个实数解,求实数k的取值范围.
查看习题详情和答案>>
| a |
| b |
| 3 |
| a |
| b |
| π |
| 2 |
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)若将y=f(x)图象上各点的横坐标变为原来的
| 1 |
| 6 |
| π |
| 3 |
| π |
| 2 |
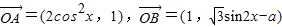 ,
,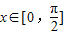 ,a为实常数,
,a为实常数,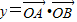
 ,求a值及此时的函数g(x)的单调增区间.
,求a值及此时的函数g(x)的单调增区间.