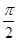题目内容
已知向量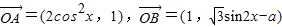 ,
,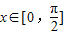 ,a为实常数,
,a为实常数,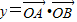
(1)求y关于x的函数解析式f(x);
(2)设函数g(x)=af(x),且g(x)的最大值是
 ,求a值及此时的函数g(x)的单调增区间.
,求a值及此时的函数g(x)的单调增区间.
【答案】分析:(1)根据向量数量积的坐标公式,结合三角恒等变换的公式加以计算,即可得到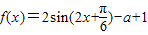 ,其中x
,其中x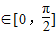 ;
;
(2)由题意,得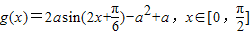 .因为
.因为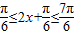 ,所以
,所以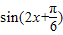 的最大值为1且最小值为-
的最大值为1且最小值为- .由此分a的正负进行讨论,结合题意建立关于a的方程,解出符合题意的a值为
.由此分a的正负进行讨论,结合题意建立关于a的方程,解出符合题意的a值为 ,得到
,得到
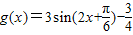 ,再根据正弦函数的单调区间公式即可算出此时的函数g(x)的单调增区间.
,再根据正弦函数的单调区间公式即可算出此时的函数g(x)的单调增区间.
解答:解(1)∵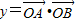 ,向量
,向量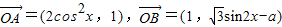 ,
,
∴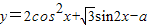 …(1分)
…(1分)
化简,可得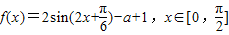 …(4分)
…(4分)
(2)由(1),可得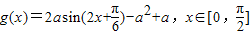 ,
,
∵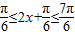 ,∴
,∴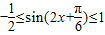 ,…(6分)
,…(6分)
①当a>0时,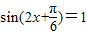 ,
,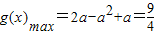 ,
,
解之得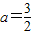 ; …(8分)
; …(8分)
②当a=0时,g(x)=0,不合题意,舍去; …(9分)
③当a<0时,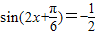 ,
,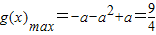 ,无解 …(10分)
,无解 …(10分)
综上所述,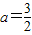 且g(x)表达式为
且g(x)表达式为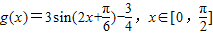 ,
,
再令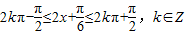 ,…(12分)
,…(12分)
解之得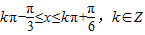 ,
,
因为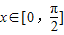 ,所以取k=0算出交集,可得函数g(x)的单调增区间为
,所以取k=0算出交集,可得函数g(x)的单调增区间为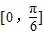 …(14分)
…(14分)
点评:本题给出向量的数量积,得到正弦型三角函数表达式,求函数的单调区间与最值.着重考查了向量的数量积运算、三角恒等变换公式和三角函数的图象与性质等知识,考查了分类讨论数学思想,属于中档题.
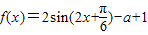 ,其中x
,其中x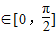 ;
;(2)由题意,得
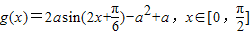 .因为
.因为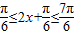 ,所以
,所以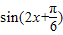 的最大值为1且最小值为-
的最大值为1且最小值为- .由此分a的正负进行讨论,结合题意建立关于a的方程,解出符合题意的a值为
.由此分a的正负进行讨论,结合题意建立关于a的方程,解出符合题意的a值为 ,得到
,得到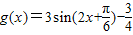 ,再根据正弦函数的单调区间公式即可算出此时的函数g(x)的单调增区间.
,再根据正弦函数的单调区间公式即可算出此时的函数g(x)的单调增区间.解答:解(1)∵
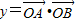 ,向量
,向量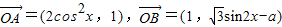 ,
,∴
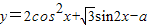 …(1分)
…(1分)化简,可得
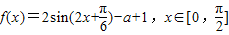 …(4分)
…(4分)(2)由(1),可得
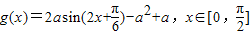 ,
,∵
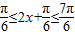 ,∴
,∴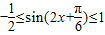 ,…(6分)
,…(6分)①当a>0时,
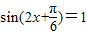 ,
,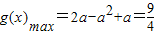 ,
,解之得
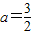 ; …(8分)
; …(8分)②当a=0时,g(x)=0,不合题意,舍去; …(9分)
③当a<0时,
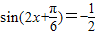 ,
,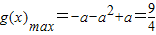 ,无解 …(10分)
,无解 …(10分)综上所述,
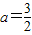 且g(x)表达式为
且g(x)表达式为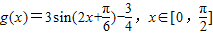 ,
,再令
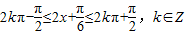 ,…(12分)
,…(12分)解之得
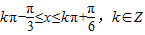 ,
,因为
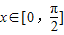 ,所以取k=0算出交集,可得函数g(x)的单调增区间为
,所以取k=0算出交集,可得函数g(x)的单调增区间为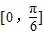 …(14分)
…(14分)点评:本题给出向量的数量积,得到正弦型三角函数表达式,求函数的单调区间与最值.着重考查了向量的数量积运算、三角恒等变换公式和三角函数的图象与性质等知识,考查了分类讨论数学思想,属于中档题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
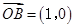 ,
,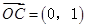 ,A为动点,
,A为动点,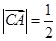 ,则
,则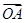 与
与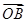 夹角的最小值为( )
夹角的最小值为( ) B.
B.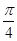 C.
C.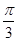 D.
D.