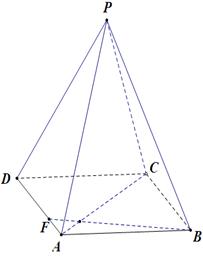
摘要:19.如图.正四棱锥P-ABCD中.AB=2.侧棱PA与底面ABCD所成的角为60°.(1)求侧面与底面所成的二面角的大小, (2)在线段PB上是否存在一点E.使得AE⊥PC.若存在.试确定点E的位置.并加以证明.若不存在.请说明理由. 解:(1)如图O为底面ABCD的中心 则∠PAO为PA与底面所成的角 ∴∠PAO=60° ∵ ∴-- 过O作OM⊥BC于M.连PM由三垂线定理得BC⊥PM ∴∠PMO为侧面与底面所成二面角平面角-- ∵OM=1.PO= --6分 (2)如图建立空间直角坐标系
网址:http://m.1010jiajiao.com/timu3_id_4464104[举报]
(本小题满分12分)
如图,在四棱锥P-ABCD中,PA⊥底面ABCD, 且底面ABCD是正方形,DM⊥PC,垂足为M.

(1)求证:BD⊥平面PAC.
(2)求证:平面MBD⊥平面PCD.
查看习题详情和答案>>
(本小题满分12分)
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD是正方形,DM⊥PC,垂足为M.
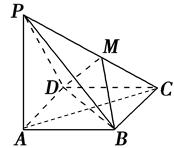
(1)求证:BD⊥平面PAC.
(2)求证:平面MBD⊥平面PCD.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD是正方形,DM⊥PC,垂足为M.

(1)求证:BD⊥平面PAC.
(2)求证:平面MBD⊥平面PCD.
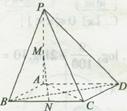
 中,AB=1,侧棱
中,AB=1,侧棱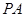 与底面
与底面 所成角的正切值为
所成角的正切值为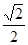 .
.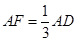 ,求点A到平面PBF的距离.
,求点A到平面PBF的距离.
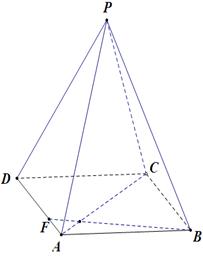
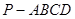 中,AB=1,侧棱
中,AB=1,侧棱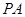 与底面
与底面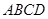 所成角的正切值为
所成角的正切值为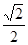 .
.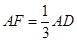 ,求点A到平面PB
,求点A到平面PB F的距离.
F的距离.