题目内容
(本小题满分12分)
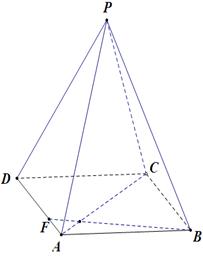
如图所示,正四棱锥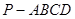
中，AB=1,侧棱
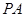与底面
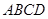所成角的正切值为
.
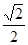（1）求二面角P-CD-A的大小.
（2）设点F在AD上,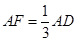
,求点A到平面PBF的距离.
【答案】
解:(1)连结AC、BD交于点O，连结PO，则PO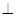 
平面ABCD
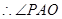就是PA与底面ABCD所成的角，
PO=AO
=
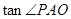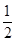
设E为CD的中点,连结PE、OE,则O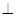ECD,
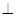PECD,
OE=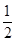
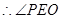就是二面角P-CD-AD的平面角
在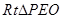
中, 
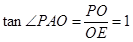,即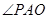
=
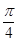
二面角P-CD-AD的大小为
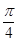
(2).过O作OM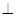BF于M,,连结PM,则由于PO 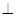平面ABCD,PM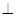BF
BF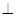平面POM,,平面POM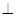平面PBF,作OH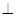P M于H,则OH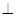平面PBF
即OH的长就等于点O到平面PBF的距离
=
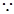
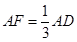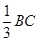,设AC与BF交于点N,则AN=
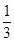NC,AN=NO
点A到平面PBF的距离就等于点O到平面PBF的距离
作AQ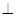BF于Q，则AQ=OM=
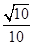在
在
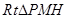中，OH=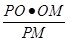
=
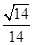
故点A到平面PBF的距离为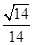
【解析】略
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
