摘要：18． 在正四棱柱ABCD-A1B1C1D1中.侧棱是底面边长的2倍.P是侧棱CC1上的任一点. (1)求证:不论P在侧棱CC1上何位置.总有BD⊥AP, (2)若CC1=3C1P.求平面AB1P与平面ABCD所成二面角的余弦值, (3)当P点在侧棱CC1上何处时.AP在平面B1AC上的射影是∠B1AC的平分线. 解(1)由题意可知.不论P点在棱CC1上的任何位置.AP在底面ABCD内射影都是 AC. . (2)延长B1P和BC.设B1P∩BC=M.连结AM.则AM=平面AB1P∩平面ABCD. 过B作BQ⊥AM于Q.连结B1Q.由于BQ是B1,Q在底面ABCD内的射影.所以B1Q⊥AM.故∠B1QB就是所求二面角的平面角.依题意.知CM=2B1C1.从而BM=3BC. 所以 . 在 中. . 得 为所求. (3)设CP=a.BC=m.则BB1=2m.C1P=2m-a.从而 在 依题意.得. . . 即 故P距C点的距离是侧棱的 别解:如图.建立空间直角坐标系. 设 依题意.得 即 故P距C点的距离是侧棱的
网址：http://m.1010jiajiao.com/timu3_id_4464081[举报]
(本小题满分12分)
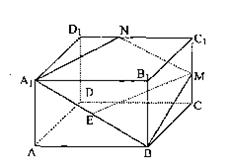如图，在正四棱柱ABCD—A1B1C1D1中，AA1=
AB，点E、M分别为A1B、C1C的中点，过点A1，B，M三点的平面A1BMN交C1D1于点N.
（Ⅰ）求证：EM∥平面A1B1C1D1；
（Ⅱ）求二面角B—A1N—B1的正切值.
查看习题详情和答案>>(本小题满分12分)
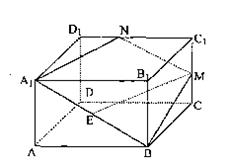
如图，在正四棱柱ABCD—A1B1C1D1中，AA1=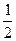
AB，点E、M分别为A1B、C1C的中点，过点A1，B，M三点的平面A1BMN交C1D1于点N.
（Ⅰ）求证：EM∥平面A1B1C1D1；
（Ⅱ）求二面角B—A1N—B1的正切值.
如图，在正四棱柱ABCD—A1B1C1D1中，AA1=
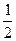AB，点E、M分别为A1B、C1C的中点，过点A1，B，M三点的平面A1BMN交C1D1于点N.（Ⅰ）求证：EM∥平面A1B1C1D1；
（Ⅱ）求二面角B—A1N—B1的正切值.
（本小题满分12分）
如图，在正四棱柱ABCD—A1B1C1D1中，AB=1，AA1=2，E为棱AA1上一点，且
平面BDE。
（I）求直线BD1与平面BDE所成角的正弦值；
（II）求二面角C—BE—D的余弦值。
查看习题详情和答案>>
平面BED
平面BED