题目内容
(本小题满分12分)
如图,在正四棱柱ABCD—A1B1C1D1中,AB=1,AA1=2,E为棱AA1上一点,且 平面BDE。
平面BDE。

(I)求直线BD1与平面BDE所成角的正弦值;
(II)求二面角C—BE—D的余弦值。
解法一:
(Ⅰ)∵C1E⊥平面BDE,
在正四棱柱ABCD—A1B1C1D1中,AB=1,AA1=2,
∴BC1=,A1C1=.
设AE=x,则BE=,C1E=,
∵BC=BE2+C1E2,∴5=1+x2+2+(2-x)2,解得x=1.……………………3分
连结D1E,由DE=EB=BD=,得
S△BDE=DE2=,S△DD1E=DD1·AD=1,
设点D1到平面BDE的距离为h,则由VD1—BDE=VB—DD1E,
得·h=·1·1,h=.
设直线BD1与平面BDE所成的角为θ,
因BD1=,则sinθ==.………………………………………………6分
(Ⅱ)分别取BE、CE的中点M、N,则MN∥BC,且MN=AB=.
∵BC⊥平面ABB1A1,BEÌ平面ABB1A1,∴BC⊥BE,∴MN⊥BE.
∵BE=BD=DE=,∴DM⊥BE,且DM=,
∴∠DMN为二面角C-BE-D的平面角.…………………………………………9分
又DN=EC=,
∴cos∠DMN==.…………………………………………12分
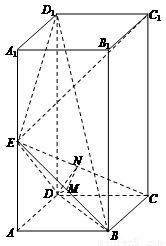

解法二:
(Ⅰ)建立如图所示的坐标系D—xyz,
其中D(0,0,0),B(1,1,0),C(0,1,0),D1(0,0,2),C1(0,1,2).设E(1,0,a),则
=(-1,1,2-a),=(1,1,0),=(1,0,a),
∵C1E⊥平面BDE,∴⊥,
∴·=-1+(2-a)a=0,解得a=1.……………………………………3分
∴=(-1,1,1).
设直线BD1与平面BDE所成的角为θ,
因=(1,1,-2),则sinθ=|\o(D1B,\s\up5(→EC1,\s\up5(→=.……………………………6分
(Ⅱ)由(Ⅰ),=(-1,1,1)为面BDE的法向量,
设n=(x,y,z)为面CBE的法向量,
∵=(1,0,0),=(0,-1,1),
∴n·=0,n·=0,
∴x=0,-y+z=0,取n=(0,1,1),…………………………………………9分
∴cosá,nñ=\o(EC1,\s\up5(→________=,
所以二面角C-BE-D的余弦值为.……………………………………………12分
【解析】略

 阅读快车系列答案
阅读快车系列答案