题目内容
(本小题满分12分)
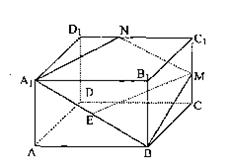 如图,在正四棱柱ABCD—A1B1C1D1中,AA1=
如图,在正四棱柱ABCD—A1B1C1D1中,AA1=![]() AB,点E、M分别为A1B、C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N.
AB,点E、M分别为A1B、C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N.
(Ⅰ)求证:EM∥平面A1B1C1D1;
(Ⅱ)求二面角B—A1N—B1的正切值.
(Ⅱ)![]()
解析:
(Ⅰ)证明:取A1B1的中点F,连EF,C1F ∵E为A1B中点 ∴EF∥ ![]() BB1 又∵M为CC1中点 ∴EF∥ C1M∴四边形EFC1M为平行四边形 ∴EM∥FC1
BB1 又∵M为CC1中点 ∴EF∥ C1M∴四边形EFC1M为平行四边形 ∴EM∥FC1
而EM ![]() 平面A1B1C1D1 . FC1
平面A1B1C1D1 . FC1![]() 平面A1B1C1D1 .
平面A1B1C1D1 .
 ∴EM∥平面A1B1C1D1………………6分
∴EM∥平面A1B1C1D1………………6分
(Ⅱ)由⑴EM∥平面A1B1C1D1
EM![]() 平面A1BMN,平面A1BMN∩平面A1B1C1D1=A1N
平面A1BMN,平面A1BMN∩平面A1B1C1D1=A1N
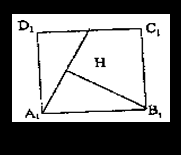
∴A1N// EM// FC1 ∴N为C1D1 中点,过B1作B1H⊥A1N于H,连BH,根据三垂线定理 BH⊥A1N
∠BHB1即为二面角B—A1N—B1的平面角……8分
设AA1=a, 则AB=2a, ∵A1B1C1D1为正方形
∴A1H=![]() 又∵△A1B1H∽△NA1D1
又∵△A1B1H∽△NA1D1
∴B1H=![]() ,在Rt△BB1H中,
,在Rt△BB1H中,
tan∠BHB1=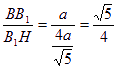 即二面角B—A1N—B1的正切值为
即二面角B—A1N—B1的正切值为![]() ……12分
……12分

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目