摘要:19. 如图. 和两点分别在射线OS.OT上移动.且.O为坐标原点.动点P满足. (Ⅰ)求的值, (Ⅱ)求P点的轨迹C的方程.并说明它表示怎样 的曲线? (Ⅲ)若直线l过点E中曲线C于M.N两 点.且.求l的方程. 解:(Ⅰ)由已知得 ----4分 (Ⅱ)设P点坐标为(x.y)(x>0).由得 ----5分 ∴ 消去m.n可得 .又因 8分 ∴ P点的轨迹方程为 它表示以坐标原点为中心.焦点在轴上.且实轴长为2.焦距为4的双曲线 的右支 ----9分 (Ⅲ)设直线l的方程为.将其代入C的方程得 即 易知(否则.直线l的斜率为.它与渐近线平行.不符合题意) 又 设.则 ∵ l与C的两个交点在轴的右侧 ∴ .即 又由 同理可得 ----11分 由得 ∴ 由得 由得 消去得 解之得: .满足 ----13分 故所求直线l存在.其方程为:或 ----14分
网址:http://m.1010jiajiao.com/timu3_id_4457010[举报]
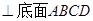
 ;
;  中,底面
中,底面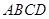 为矩形,侧棱
为矩形,侧棱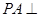 底面
底面 为
为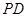 的中点.
的中点.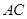 与
与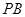 所成角的余弦值;
所成角的余弦值;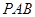 内找一点
内找一点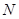 ,使
,使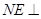 平面
平面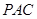 ,并分别求出点
,并分别求出点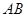 和
和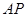 的距离.
的距离.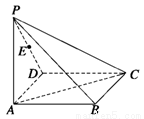
 中,
中, ,点
,点 在边
在边 上,
上, 。
。 平面
平面 ;
; 是
是 的中点,求证:
的中点,求证: 平面
平面 .
.
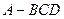 中,
中,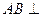 平面
平面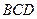 ,
,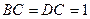 ,
,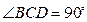 ,
,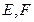 分别是
分别是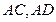 上
上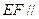 平面
平面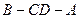 为
为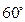 .
.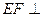 平面
平面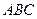 ;
;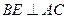 ,求直线
,求直线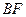 与平面
与平面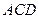 所成角的余弦值.
所成角的余弦值.