（几何证明选讲选做题）
如图，AB为⊙O的直径，弦AC、BD相交于点P，若AB=3，CD=1，则cos∠BPC的值为．

（2012•福建模拟）阅读下面材料：
根据两角和与差的正弦公式，有sin（α+β）=sinαcosβ+cosαsinβ------①
sin（α-β）=sinαcosβ-cosαsinβ------②
由①+②得sin（α+β）+sin（α-β）=2sinαcosβ------③
令α+β=A，α-β=B有α=

A+B

2

，β=

A-B

2

代入③得 sinA+sinB=2sin

A+B

2

cos

A-B

2

．
（Ⅰ）类比上述推证方法，根据两角和与差的余弦公式，证明：cosA-cosB=-2sin

A+B

2

sin

A-B

2

；
（Ⅱ）若△ABC的三个内角A，B，C满足cos2A-cos2B=2sin²C，试判断△ABC的形状．
（提示：如果需要，也可以直接利用阅读材料及（Ⅰ）中的结论）

请考生在下列两题中任选一题作答，若两题都做，则按所做的第一题评阅计分．
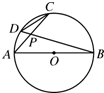1（1）．（几何证明选讲选做题）如图，四边形ABCD是圆O的内接四边形，
延长AB和DC相交于点P，若

PB

PA

=

1

2

，

PC

PD

=

1

3

，则

BC

AD

的值为．
（2）．（坐标系与参数方程选做题） 极坐标系中，A为曲线ρ²+2ρcosθ-3=0上
的动点，B为直线ρcosθ+ρsinθ-7=0的动点，则|AB|距离的最小值为．