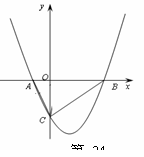
摘要:9.抛物线与轴交于A.B两点.与轴交于正半轴C点.且AC = 20.BC = 15.∠ACB = 90°.则此抛物线的解析式为 ,
网址:http://m.1010jiajiao.com/timu3_id_442626[举报]
如图,抛物线与![]() 轴交于
轴交于![]() (
(![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() (
(![]() 设抛物线的顶点为
设抛物线的顶点为![]() .
.
(1)求该抛物线的解析式与顶点![]() 的坐标.
的坐标.
(2)试判断△![]() 的形状,并说明理由.
的形状,并说明理由.
(3)探究坐标轴上是否存在点![]() ,使得以
,使得以![]() 为顶点的三角形与△
为顶点的三角形与△![]() 相似?
相似?
若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 |
查看习题详情和答案>>
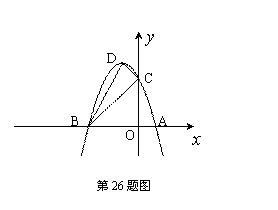
如图,抛物线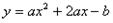 与
与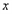 轴交于
轴交于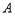 、
、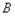 两点,与
两点,与 轴正半轴交于
轴正半轴交于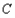 点,且
点,且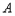 (
(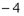 ,0),
,0),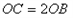
(1)求出抛物线的解析式;
(2)如图①,作矩形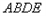 ,使
,使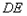 过点
过点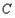 ,点
,点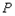 是
是 边上的一动点,连接
边上的一动点,连接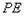 ,作
,作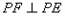 交
交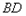 于点
于点 ,设线段
,设线段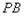 的长为
的长为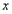 ,线段
,线段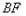 的长为
的长为 ,当
,当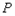 点运动时,求
点运动时,求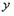 与
与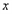 的函数关系式并写出自变量
的函数关系式并写出自变量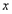 的取值范围,在同一直角坐标系中,该函数的图象与图①的抛物线中
的取值范围,在同一直角坐标系中,该函数的图象与图①的抛物线中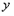 ≥0的部分有何关系?
≥0的部分有何关系?
(3)如图②,在图①的抛物线中,点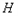 为其顶点,
为其顶点,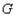 为抛物线上一动点(不与
为抛物线上一动点(不与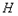 重合),取点
重合),取点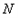 (
(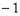 ,0),作
,0),作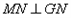 且
且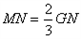 (点
(点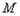 、
、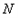 、
、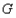 按逆时针顺序),当点
按逆时针顺序),当点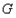 在抛物线上运动时,直线
在抛物线上运动时,直线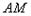 、
、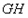 是否存在某种位置关系?若存在,写出并证明你的结论;若不存在,请说明理由。
是否存在某种位置关系?若存在,写出并证明你的结论;若不存在,请说明理由。
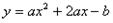 与
与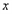 轴交于
轴交于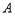 、
、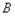 两点,与
两点,与 轴正半轴交于
轴正半轴交于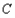 点,且
点,且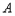 (
(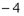 ,0),
,0),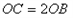
(1)求出抛物线的解析式;
(2)如图①,作矩形
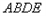 ,使
,使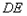 过点
过点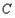 ,点
,点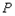 是
是 边上的一动点,连接
边上的一动点,连接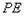 ,作
,作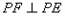 交
交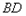 于点
于点 ,设线段
,设线段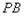 的长为
的长为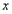 ,线段
,线段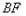 的长为
的长为 ,当
,当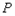 点运动时,求
点运动时,求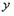 与
与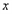 的函数关系式并写出自变量
的函数关系式并写出自变量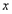 的取值范围,在同一直角坐标系中,该函数的图象与图①的抛物线中
的取值范围,在同一直角坐标系中,该函数的图象与图①的抛物线中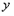 ≥0的部分有何关系?
≥0的部分有何关系?(3)如图②,在图①的抛物线中,点
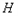 为其顶点,
为其顶点,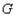 为抛物线上一动点(不与
为抛物线上一动点(不与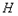 重合),取点
重合),取点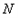 (
(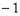 ,0),作
,0),作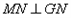 且
且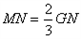 (点
(点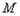 、
、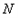 、
、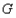 按逆时针顺序),当点
按逆时针顺序),当点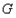 在抛物线上运动时,直线
在抛物线上运动时,直线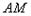 、
、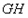 是否存在某种位置关系?若存在,写出并证明你的结论;若不存在,请说明理由。
是否存在某种位置关系?若存在,写出并证明你的结论;若不存在,请说明理由。
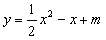 与
与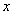 轴交于
轴交于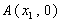 、
、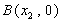 ,
,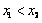 ,且
,且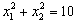 ,点D是抛物线的顶点。
,点D是抛物线的顶点。