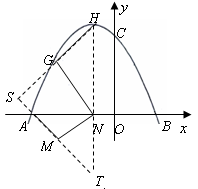
题目内容
如图,抛物线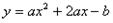 与
与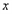 轴交于
轴交于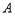 、
、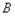 两点,与
两点,与 轴正半轴交于
轴正半轴交于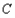 点,且
点,且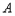 (
(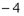 ,0),
,0),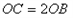
(1)求出抛物线的解析式;
(2)如图①,作矩形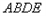 ,使
,使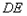 过点
过点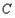 ,点
,点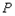 是
是 边上的一动点,连接
边上的一动点,连接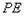 ,作
,作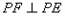 交
交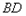 于点
于点 ,设线段
,设线段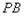 的长为
的长为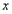 ,线段
,线段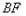 的长为
的长为 ,当
,当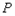 点运动时,求
点运动时,求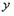 与
与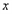 的函数关系式并写出自变量
的函数关系式并写出自变量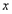 的取值范围,在同一直角坐标系中,该函数的图象与图①的抛物线中
的取值范围,在同一直角坐标系中,该函数的图象与图①的抛物线中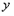 ≥0的部分有何关系?
≥0的部分有何关系?
(3)如图②,在图①的抛物线中,点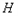 为其顶点,
为其顶点,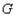 为抛物线上一动点(不与
为抛物线上一动点(不与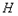 重合),取点
重合),取点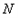 (
(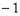 ,0),作
,0),作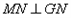 且
且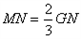 (点
(点 、
、 、
、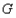 按逆时针顺序),当点
按逆时针顺序),当点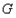 在抛物线上运动时,直线
在抛物线上运动时,直线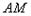 、
、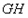 是否存在某种位置关系?若存在,写出并证明你的结论;若不存在,请说明理由。
是否存在某种位置关系?若存在,写出并证明你的结论;若不存在,请说明理由。
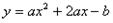 与
与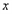 轴交于
轴交于 、
、 两点,与
两点,与 轴正半轴交于
轴正半轴交于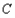 点,且
点,且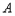 (
(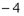 ,0),
,0),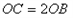
(1)求出抛物线的解析式;
(2)如图①,作矩形
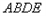 ,使
,使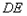 过点
过点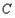 ,点
,点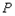 是
是 边上的一动点,连接
边上的一动点,连接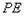 ,作
,作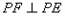 交
交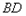 于点
于点 ,设线段
,设线段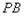 的长为
的长为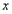 ,线段
,线段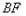 的长为
的长为 ,当
,当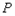 点运动时,求
点运动时,求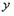 与
与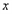 的函数关系式并写出自变量
的函数关系式并写出自变量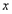 的取值范围,在同一直角坐标系中,该函数的图象与图①的抛物线中
的取值范围,在同一直角坐标系中,该函数的图象与图①的抛物线中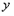 ≥0的部分有何关系?
≥0的部分有何关系?(3)如图②,在图①的抛物线中,点
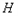 为其顶点,
为其顶点,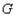 为抛物线上一动点(不与
为抛物线上一动点(不与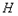 重合),取点
重合),取点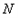 (
(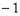 ,0),作
,0),作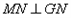 且
且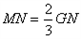 (点
(点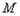 、
、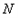 、
、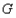 按逆时针顺序),当点
按逆时针顺序),当点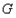 在抛物线上运动时,直线
在抛物线上运动时,直线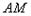 、
、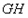 是否存在某种位置关系?若存在,写出并证明你的结论;若不存在,请说明理由。
是否存在某种位置关系?若存在,写出并证明你的结论;若不存在,请说明理由。
解:(1)∵ ,
,
∴抛物线的对称轴为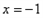 ,
,
∵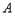 (
(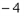 ,0),∴
,0),∴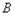 (2,0)
(2,0)
∴ ,∴
,∴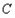 (0,4)
(0,4)
∴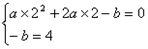 ,
,
∴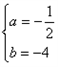 ,
,
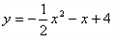
(2)∵四边形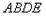 为矩形,
为矩形,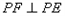 ,
,
∴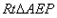 ∽
∽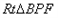
∴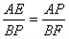 ,即
,即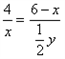 ,
,
∴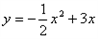 ,(
,(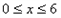 )
)
又∵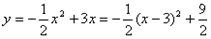 ,
,
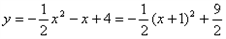 ,
,
∴图①的抛物线中,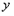 ≥0时,
≥0时, ,
,
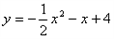 中
中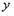 ≥0的部分向右平移4个单位得到
≥0的部分向右平移4个单位得到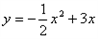 (
(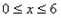 ).
).
(3) ,理由如下:
,理由如下:
连接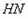 并延长交
并延长交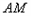 延长线于点
延长线于点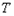 ,设直线
,设直线 、
、 交于点
交于点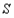 ,
,
∵点H为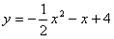 抛物线的顶点,
抛物线的顶点,
∴H( ,
,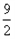 ),
),
且A(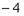 ,0),
,0), (
(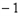 ,0),
,0),
∴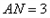
∴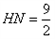 ,
,
∵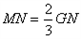 ,且
,且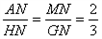
∵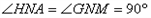 ,
,
∵ ,
,
∴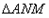 ∽
∽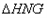 ,
,
∴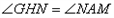
∴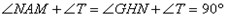
∴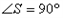 ,则
,则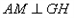
 ,
,∴抛物线的对称轴为
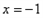 ,
,∵
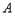 (
(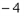 ,0),∴
,0),∴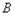 (2,0)
(2,0)∴
 ,∴
,∴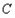 (0,4)
(0,4)∴
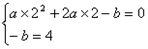 ,
,∴
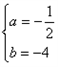 ,
, 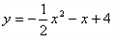
(2)∵四边形
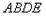 为矩形,
为矩形,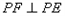 ,
,∴
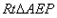 ∽
∽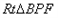
∴
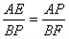 ,即
,即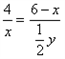 ,
,∴
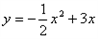 ,(
,(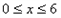 )
)又∵
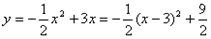 ,
,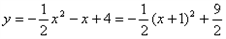 ,
,∴图①的抛物线中,
 ≥0时,
≥0时, ,
,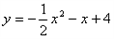 中
中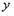 ≥0的部分向右平移4个单位得到
≥0的部分向右平移4个单位得到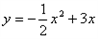 (
(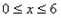 ).
).(3)
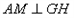 ,理由如下:
,理由如下:连接
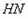 并延长交
并延长交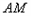 延长线于点
延长线于点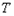 ,设直线
,设直线 、
、 交于点
交于点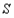 ,
,∵点H为
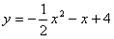 抛物线的顶点,
抛物线的顶点,∴H(
 ,
,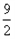 ),
),且A(
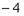 ,0),
,0), (
(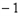 ,0),
,0),∴
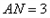
∴
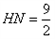 ,
,∵
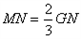 ,且
,且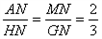
∵
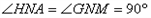 ,
,∵
 ,
,∴
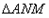 ∽
∽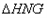 ,
,∴
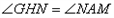
∴
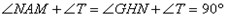
∴
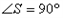 ,则
,则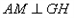


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 轴交于
轴交于 (2)点
(2)点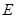 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以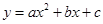 与
与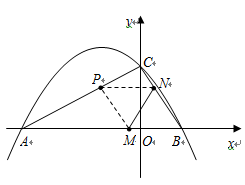
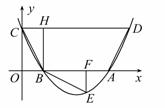
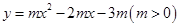 与
与 轴交于
轴交于 两点,与
两点,与 轴交于
轴交于 点.
点.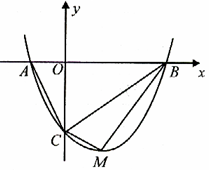
 的坐标(用含
的坐标(用含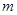 的代数式表示),
的代数式表示), 与
与 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;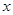 轴交于
轴交于 (
( ,0)、
,0)、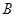 (
( ,0)两点,且
,0)两点,且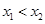 ,与
,与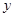 轴交于点
轴交于点 ,其中
,其中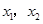 是方程
是方程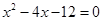 的两个根。(14分)
的两个根。(14分) (2)点
(2)点 是线段
是线段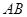 上的一个动点,过点
上的一个动点,过点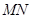 ∥
∥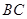 ,交
,交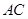 于点
于点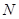 ,连接
,连接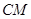 ,当
,当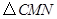 的面积最大时,求点
的面积最大时,求点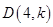 在(1)中抛物线上,
在(1)中抛物线上,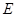 为抛物线上一动点,在
为抛物线上一动点,在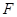 ,使以
,使以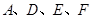 为顶
为顶