题目内容
如图,已知抛物线 与直线
与直线 交于点O(0,0),
交于点O(0,0),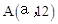 。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。
。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。

(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造条形BCDE,设点D的坐标为(m,n),求m,n之间的关系式。
【答案】
解:(1)∵点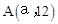 在直线
在直线 上,∴
上,∴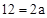 ,即
,即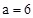 。
。
∴点A的坐标是(6,12)。
又∵点A(6,12)在抛物线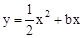 上,
上,
∴把A(6,12)代入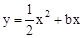 ,得
,得 。
。
∴抛物线的函数解析式为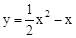 。
。
(2)∵点C为OA的中点,∴点C的坐标是(3,6)。
把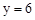 代入
代入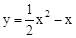 ,解得
,解得 (舍去)。
(舍去)。
∴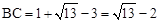 。
。
(3)∵点D的坐标为(m,n),∴点E的坐标为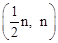 ,点C的坐标为
,点C的坐标为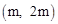 。
。
∴点B的坐标为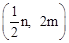 。
。
把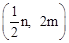 代入
代入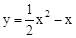 ,得
,得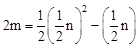 ,即
,即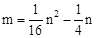 。
。
∴m,n之间的关系式为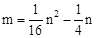 。
。
【解析】(1)根据点在曲线上,点的坐标满足于方程的关系,先求得由点A在直线 上求得点A的坐标,再由点A在抛物线
上求得点A的坐标,再由点A在抛物线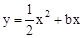 上,求得
上,求得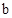 ,从而得到抛物线的函数解析式。
,从而得到抛物线的函数解析式。
(2)由于点B,C的纵坐标相等,从而由点C为OA的中点求得点C的坐标,将其纵坐标代入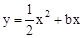 ,求得
,求得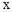 ,即可得到BC的长。
,即可得到BC的长。
(3)根据题意求出点B的坐标,代入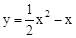 即可求得m,n之间的关系式。
即可求得m,n之间的关系式。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
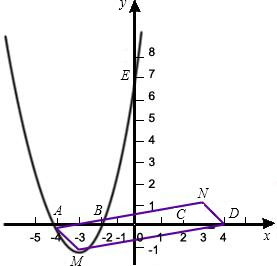 如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
 与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
 关于原点对称的抛物线
关于原点对称的抛物线 的解析式;
的解析式; 与x轴分别交于C、D两点(点C在点D的左侧),顶点为N,四边形MDNA的面积为S.若点A、点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点M、点N同时以每秒2个单位的速度沿竖直方向分别向下、向上运动,直到点A与点D重合为止.求出四边形MDNA的面积S与运动时间t之间的关系式,并写出自变量t的取值范围;
与x轴分别交于C、D两点(点C在点D的左侧),顶点为N,四边形MDNA的面积为S.若点A、点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点M、点N同时以每秒2个单位的速度沿竖直方向分别向下、向上运动,直到点A与点D重合为止.求出四边形MDNA的面积S与运动时间t之间的关系式,并写出自变量t的取值范围;
