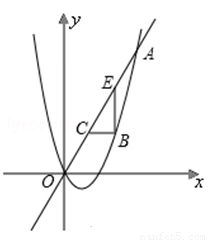
题目内容
如图,已知抛物线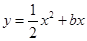 与直线
与直线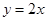 交于点
交于点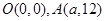 .点
.点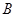 是抛物线上
是抛物线上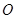 ,
,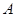 之间的一个动点,过点
之间的一个动点,过点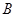 分别作
分别作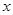 轴、
轴、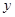 轴的平行线与直线
轴的平行线与直线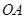 交于点
交于点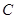 ,
,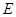 .
.
(1)求抛物线的函数解析式;
(2)若点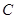 的横坐标为2,求
的横坐标为2,求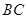 的长;
的长;
(3)以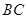 ,
,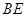 为边构造矩形
为边构造矩形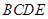 ,设点
,设点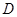 的坐标为
的坐标为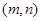 ,求出
,求出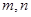 之间的关系式.
之间的关系式.
【答案】
(1)抛物线解析式为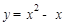 ;(2)
;(2)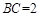 ;(3)
;(3)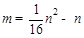 .
.
【解析】
试题分析:(1)由点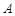 的坐标在直线
的坐标在直线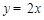 上,可求得该点坐标.将该点坐标代入抛物线函数中;(2)可先求得
上,可求得该点坐标.将该点坐标代入抛物线函数中;(2)可先求得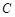 点坐标,然后求取
点坐标,然后求取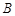 点坐标,则
点坐标,则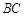 长可求;(3)由点
长可求;(3)由点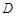 的坐标可推出点
的坐标可推出点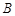 的坐标,依据抛物线的函数式,将含
的坐标,依据抛物线的函数式,将含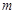 ,
,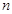 的点
的点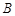 坐标代入函数式,可得
坐标代入函数式,可得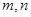 之间的关系式.
之间的关系式.
试题解析:(1)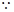 点
点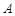
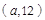 在直线
在直线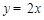 上,
上,
∴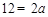 ,解得:
,解得: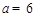 ,
,
又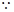 点
点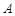 是抛物线
是抛物线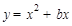 上的一点,将点
上的一点,将点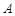
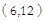 代入
代入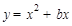 ,可得
,可得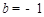 ,
,
∴抛物线解析式为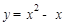 .
.
(2) 点
点 的横坐标为2,
的横坐标为2, 点
点 的坐标为
的坐标为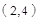 ,
,
把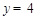 代入
代入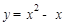 ,解得:
,解得: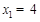 ,
, (舍去),故
(舍去),故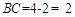 .
.
(3) 点
点 的坐标为
的坐标为 ,
,
∴点 的坐标为
的坐标为 ,点C的坐标为
,点C的坐标为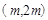 ,
,
∴点B的坐标为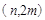 ,
,
把点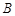
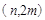 代入
代入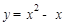 ,可得
,可得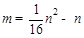 ,
,
∴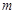 、
、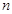 之间的关系式为
之间的关系式为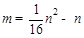 ..
..
【考点】1.二次函数的图形;2.二次函数解析式的求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
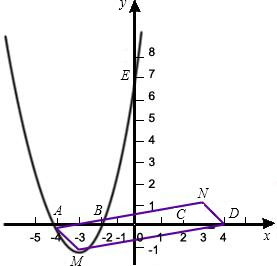 如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
 与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
 关于原点对称的抛物线
关于原点对称的抛物线 的解析式;
的解析式; 与x轴分别交于C、D两点(点C在点D的左侧),顶点为N,四边形MDNA的面积为S.若点A、点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点M、点N同时以每秒2个单位的速度沿竖直方向分别向下、向上运动,直到点A与点D重合为止.求出四边形MDNA的面积S与运动时间t之间的关系式,并写出自变量t的取值范围;
与x轴分别交于C、D两点(点C在点D的左侧),顶点为N,四边形MDNA的面积为S.若点A、点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点M、点N同时以每秒2个单位的速度沿竖直方向分别向下、向上运动,直到点A与点D重合为止.求出四边形MDNA的面积S与运动时间t之间的关系式,并写出自变量t的取值范围;
