如图所示，在水平地面上固定一倾角θ=37°的斜面体，物体A以某一初速度从斜面体底端沿斜面向上抛出，在物体A的正上方，有一物体B以某一初速度水平抛出．A、B均可看作质点，已知sin37°=0.6，cos37°=0.8，g取10m/s²．
（1）若斜面体表面光滑，将A物体以v₁=6m/s的初速度抛出，求物体A上滑到最高点所用的时间t．
（2）在第（1）问条件下，将A、B同时抛出，当A上滑到最高点时恰好被B物体击中，求物体B抛出时的初速度v₂．
（3）若斜面体表面粗糙且足够长，物体A与斜面间的动摩擦因数μ=0.5，物体A从最低点以v₃=10m/s的初速度沿斜面向上抛出，B仍以初速度v₂水平抛出，为使B抛出后仍能击中A，求A、B开始运动时相差的时间间隔 （结果可保留根号）．

如图所示是放置在竖直平面内的游戏滑轨，有一质量m=2kg的小球穿在轨道上．滑轨由四部分粗细均匀的滑杆组成；水平轨道AB；与水平面间的成夹角θ=37⁰且长L=6m的倾斜直轨道CD；半径R=1m的圆弧轨道APC；半径R=3m的圆弧轨道BQED．直轨道与圆弧轨道相切，切点分别为A、B、D、C，E为最低点．倾斜轨道CD与小球间的动摩擦因数μ=

5

32

，其余部分均为光滑轨道，取g=10m/s²，sin37°=0.6，cos37°=0.8．现让小球从AB的正中央以初速度v₀=10m/s开始向左运动，问：
（1）第一次经过E处时，轨道对小球的作用力为多大？
（2）小球第一次经过C点时的速度为多大？
（3）小球在运动过程中，损失的机械能最多为多少？

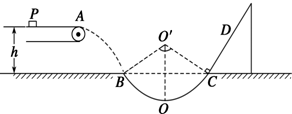如图所示，水平传送带以5m/s的速度沿顺时针方向运动，在传送带上的P点轻轻地放上一质量m=1kg的小物块，PA间的距离为1.5m，小物块随传送带运动到A点后水平抛出，恰好沿圆弧切线从B点进入竖直光滑圆弧轨道运动．B、C为圆弧的两端点其连线水平，CD为与C点相切的一固定斜面．小物块离开C点后经0.8s通过D点．已知小物块与传送带间的动摩擦因数μ₁=0.3，圆弧轨道最低点为O，A点与水平面的高度差h=0.8m，小物块与斜面间的动摩擦因数μ₂=

1

3

，sin 37°=0.6，cos 37°=0.8，g取10m/s²．试求：
（1）小物块离开A点时的速度大小；
（2）圆弧BOC对应的圆心角θ为多少？
（3）斜面上CD间的距离．

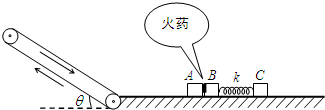如图所示，倾角θ=37°的粗糙传送带与光滑水平面通过半径可忽略的光滑小圆弧平滑连接，传送带始终以v=3m/s的速率顺时针匀速转动，A、B、C滑块的质量为 m_A=1kg，m_B=2kg，m_C=3kg，（各滑块均视为质点）．A、B间夹着质量可忽略的火药．k为处于原长的轻质弹簧，两端分别与B和C连接．现点燃火药（此时间极短且不会影响各物体的质量和各表面的光滑程度），滑块A以6m/s水平向左冲出，接着沿传送带向上前进，已知滑块A与传送带间的动摩擦因数为μ=0.75，传送带与水平面足够长，取g=10m/s²，sin37°=0.6，cos37°=0.8．求：
（1）滑块A沿传送带向上能滑的最大距离？
（2）滑块B通过弹簧与C相互作用的过程中，弹簧又到原长时B、C的速度？
（3）滑块A追上滑块B时能粘住，试定量分析在A与B相遇的各种可能情况下，A、B、C及弹簧组成系统的机械能范围？

如图所示，装置BO′O可绕竖直轴O′O转动，可视为质点的小球A与两细线连接后分别系于B、C两点，装置静止时细线AB水平，细线AC与竖直方向的夹角θ=37°．已知小球的质量m=1kg，细线AC长L=1m，B点距转轴的水平距离和距C点竖直距离相等．（重力加速度g取10m/s²，sin37°=0.6，cos37°=0.8）

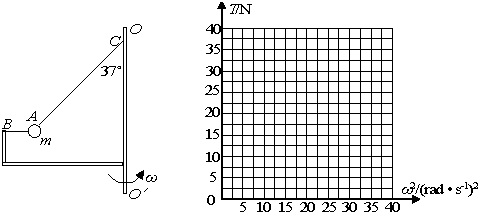
（1）若装置匀速转动的角速度为ω₁时，细线AB上的张力为0而细线AC与竖直方向的夹角仍为37°，求角速度ω₁的大小；
（2）若装置匀速转动的角速度为ω₂时，细线AB刚好竖直，且张力为0，求此时角速度ω₂的大小；
（3）装置可以以不同的角速度匀速转动，试通过计算在坐标图中画出细线AC上张力T随角速度的平方ω²变化的关系图象．