摘要: 如图3所示.曲线上任一点P(.)的速度方向反向延长线交于轴上的A点.由图3可知.所以OA=.
网址:http://m.1010jiajiao.com/timu3_id_1526100[举报]
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在xOy平面的第一象限,存在以x轴、y轴及双曲线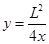 的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,则:
的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,则:
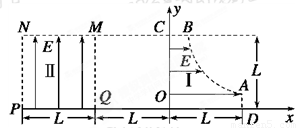
(1)求从电场区域Ⅰ的边界B点(B点的纵坐标为L)处由静止释放电子,到达区域Ⅱ的M点时的速度;
(2) 求(1)中的电子离开MNPQ时的坐标;
(3)证明在电场区域Ⅰ的AB曲线上任何一点处,由静止释放电子恰能从MNPQ区域左下角P点离开;
查看习题详情和答案>>
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在xOy平面的第一象限,存在以x轴、y轴及双曲线 的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,则:
的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,则:
(1)求从电场区域Ⅰ的边界B点(B点的纵坐标为L)处由静止释放电子,到达区域Ⅱ的M点时的速度;
(2) 求(1)中的电子离开MNPQ时的坐标;
(3)证明在电场区域Ⅰ的AB曲线上任何一点处,由静止释放电子恰能从MNPQ区域左下角P点离开;
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在xOy平面的第一象限,存在以x轴、y轴及双曲线 的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,则:
的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,则:

(1)求从电场区域Ⅰ的边界B点(B点的纵坐标为L)处由静止释放电子,到达区域Ⅱ的M点时的速度;
(2) 求(1)中的电子离开MNPQ时的坐标;
(3)证明在电场区域Ⅰ的AB曲线上任何一点处,由静止释放电子恰能从MNPQ区域左下角P点离开;
 的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,则:
的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,则:
(1)求从电场区域Ⅰ的边界B点(B点的纵坐标为L)处由静止释放电子,到达区域Ⅱ的M点时的速度;
(2) 求(1)中的电子离开MNPQ时的坐标;
(3)证明在电场区域Ⅰ的AB曲线上任何一点处,由静止释放电子恰能从MNPQ区域左下角P点离开;
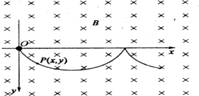 在场强为B的水平匀强磁场中,一质量为m、带正电q的小球在O静止释放,小球的运动曲线如图所示.已知此曲线在最低点的曲率半径为该点到z轴距离的2倍,重力加速度为g.求:
在场强为B的水平匀强磁场中,一质量为m、带正电q的小球在O静止释放,小球的运动曲线如图所示.已知此曲线在最低点的曲率半径为该点到z轴距离的2倍,重力加速度为g.求: 

 )的匀强电场时,小球从O静止释放后获得的最大速率
)的匀强电场时,小球从O静止释放后获得的最大速率 .
.