题目内容
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在xOy平面的第一象限,存在以x轴、y轴及双曲线 的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,则:
的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ;在第二象限存在以x=-L、x=-2L、y=0、y=L的匀强电场区域Ⅱ.两个电场大小均为E,不计电子所受重力,电子的电荷量为e,则:
(1)求从电场区域Ⅰ的边界B点(B点的纵坐标为L)处由静止释放电子,到达区域Ⅱ的M点时的速度;
(2) 求(1)中的电子离开MNPQ时的坐标;
(3)证明在电场区域Ⅰ的AB曲线上任何一点处,由静止释放电子恰能从MNPQ区域左下角P点离开;
(1) v= ;(2)(-2L,0);
;(2)(-2L,0);
(3)离开点的横坐标X1=-2L,纵坐标y1=y-y’=0,即(-2L,0)为P点。
解析试题分析: (1) B点坐标( , L),在电场I中电子被加速到v,由动能定理
, L),在电场I中电子被加速到v,由动能定理
eE =
= ,解得v=
,解得v=
(2)电子进入电场II做类平抛运动,有
t= ;
;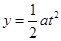 ;
;
所以横坐标x=" -" 2L;纵坐标y=L-y=0即为(-2L,0)
(3)设释放点在电场区域I的AB曲线边界,其坐标为(x,y),在电场I中电子被加速到v1,然后进入电场II做类平抛运动,有eEx= ;t=
;t= ;
; ;
;
所以离开点的横坐标X1=-2L,纵坐标y1=y-y’=0,即(-2L,0)为P点。
考点: 带电粒子在电场中的运动

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 、
、 为两正对的圆形金属板,两板间距为
为两正对的圆形金属板,两板间距为 ,板的半径为
,板的半径为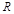 ,且
,且 。当
。当 的细束紫外线照射时,照射部位发射沿不同方向运动的光电子,形成光电流,从而引起电流表的指针偏转。已知普朗克常量h、电子电荷量e、电子质量m。
的细束紫外线照射时,照射部位发射沿不同方向运动的光电子,形成光电流,从而引起电流表的指针偏转。已知普朗克常量h、电子电荷量e、电子质量m。
 时,电流恰好为零。求:
时,电流恰好为零。求: ;
; 之后,电流便趋于饱和。求此电压
之后,电流便趋于饱和。求此电压
 时刻释放该带电粒子,释放瞬间粒子加速度的大小;
时刻释放该带电粒子,释放瞬间粒子加速度的大小;

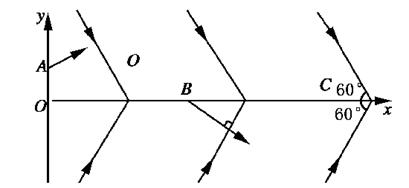

 cm,板长L=1.0cm,带电粒子质量m=2.0×10-25kg,电量q=8.0×10-18C,入射速度v =
cm,板长L=1.0cm,带电粒子质量m=2.0×10-25kg,电量q=8.0×10-18C,入射速度v = ×105m/s.若能在荧光屏上观察到亮点,试求粒子在磁场中运动的轨道半径r,并确定磁场区域的半径R应满足的条件.
×105m/s.若能在荧光屏上观察到亮点,试求粒子在磁场中运动的轨道半径r,并确定磁场区域的半径R应满足的条件. 时刻以速度v0射入电场,要使该电子能通过平行金属板,试确定U0应满足的条件.
时刻以速度v0射入电场,要使该电子能通过平行金属板,试确定U0应满足的条件.
