摘要:11.用如图所示装置来验证动量守恒定律.质量为mA的钢球A用细线悬挂于O点.质量为mB的钢球B放在离地面高度为H的小支柱N上.O点到A球球心的距离为L.使悬线在A球释放前伸直.且线与竖直线夹角为.A球释放后摆到最低点时恰与B球正碰.碰撞后.A球把轻质指示针OC推移到与竖直线夹角β处.B球落到地面上.地面上铺有一张盖有复写纸的白纸D.保持α角度不变.多次重复上述实验.白纸上记录到多个B球的落点. (1)图中S应是B球初始位置到 的水平距离. (2)为了验证两球碰撞过程动量守恒.应测得的物理量有 . (3)用测得的物理量表示碰撞前后A球.B球的动量:PA= .PA/= .PB= .PB/= .
网址:http://m.1010jiajiao.com/timu3_id_1364568[举报]
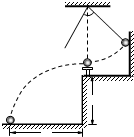 用如图所示装置来验证动量守恒定律,质量为mB的钢球B放在小支柱N上,离地面高度为H;质量为mA的钢球A用细线拴好悬挂于O点,当细线被拉直时O点到球心的距离为L,且细线与竖直线之间夹角为α;球A由静止释放,摆到最低点时恰与球B发生正碰,碰撞后,A球把轻质指示针C推移到与竖直夹角为β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸D,用来记录球 B 的落点.
用如图所示装置来验证动量守恒定律,质量为mB的钢球B放在小支柱N上,离地面高度为H;质量为mA的钢球A用细线拴好悬挂于O点,当细线被拉直时O点到球心的距离为L,且细线与竖直线之间夹角为α;球A由静止释放,摆到最低点时恰与球B发生正碰,碰撞后,A球把轻质指示针C推移到与竖直夹角为β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸D,用来记录球 B 的落点.用图中所示各个物理量的符号表示碰撞前后两球A、B的动量(设两球A、B碰前的动量分别为pA、pB; 碰后动量分别为 PA′、PB′,则PA=
mA
| 2gL(1-cosα) |
mA
,PA′=| 2gL(1-cosα) |
mA
| 2gL(1-cosβ) |
mA
,PB=| 2gL(1-cosβ) |
0
0
,PB′=mBS
|
mBS
.
|
 用如图所示装置来验证动量守恒定律,质量为mA的小钢球A用细线悬挂于O点,质量为mB的钢球B放在O点正下方离地面高度为H的小支柱N上,A球的悬线长度为L,使悬线在A球释放前伸直,且线与竖直线夹角为α,A球释放后摆到最低点时恰与B球正碰,碰撞后,A球把轻质指示针OC推移到与竖直线夹角β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸D,保持α角度不变,多次重复上述实验,白纸上记录到多个B
用如图所示装置来验证动量守恒定律,质量为mA的小钢球A用细线悬挂于O点,质量为mB的钢球B放在O点正下方离地面高度为H的小支柱N上,A球的悬线长度为L,使悬线在A球释放前伸直,且线与竖直线夹角为α,A球释放后摆到最低点时恰与B球正碰,碰撞后,A球把轻质指示针OC推移到与竖直线夹角β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸D,保持α角度不变,多次重复上述实验,白纸上记录到多个B球的落点.
(1)为了验证两球碰撞过程动量守恒,应测得的物理量有A球的质量mA,B球的质量mB,A球刚释放时细线与竖直方向的夹角α,碰撞后,A球把轻质指示针OC推移到与竖直线夹角β和B球落点的水平位移s外,还应测出
H
H
和L
L
.(用题中所给的字母表示)(2)用测得的物理量表示碰撞前A球的动量PA
=mA
| 2gL(1-cosα) |
=mA
和碰撞后B球的动量P′B| 2gL(1-cosα) |
=mBs
|
=mBs
.(当地的重力加速度g为已知)
|
 用如图所示装置来验证动量守恒定律,质量为mB的钢球B放在小支柱N上,球心离地面高度为H;质量为mA的钢球A用细线拴好悬挂于O点,当细线被拉直时O点到球心的距离为L,且细线与竖直线之间夹角α;球A由静止释放,摆到最低点时恰与球B发生正碰,碰撞后,A球把轻质指示针C推移到与竖直夹角为β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸D,用来记录球B的落点.
用如图所示装置来验证动量守恒定律,质量为mB的钢球B放在小支柱N上,球心离地面高度为H;质量为mA的钢球A用细线拴好悬挂于O点,当细线被拉直时O点到球心的距离为L,且细线与竖直线之间夹角α;球A由静止释放,摆到最低点时恰与球B发生正碰,碰撞后,A球把轻质指示针C推移到与竖直夹角为β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸D,用来记录球B的落点.(1)为了保证球A把球B弹出后能继续向前摆动,应该满足的关系是mA
大于
大于
mB(2)用图中所示各个物理量的符号表示碰撞前后两球A、B的动量(设两球A、B碰前的动量分别为PA、PB;碰后动量分别为
| P | ′ A |
| P | ′ B |
mA
| 2gl(1-cosα) |
mA
;| 2gl(1-cosα) |
| P | ′ A |
mA
| 2gl(1-cosβ) |
mA
;PB=| 2gl(1-cosβ) |
0
0
;| P | ′ B |
mBS
|
mBS
.
|
 用如图所示装置来验证动量守恒定律,质量为mB的钢球B放在小支柱上,球心离地面高度为H;质量为mA的钢球A用细线栓好悬挂于O点,当细线被拉直时O点到球心的距离为L,且细线与竖直线之间夹角为α;A球由静止释放,摆到最低点时恰与B球发生正碰,碰撞后,A球把轻质指示针C推移到与竖直线夹角为β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸,用来记录B球的落点.B球飞行的水平距离为S.
用如图所示装置来验证动量守恒定律,质量为mB的钢球B放在小支柱上,球心离地面高度为H;质量为mA的钢球A用细线栓好悬挂于O点,当细线被拉直时O点到球心的距离为L,且细线与竖直线之间夹角为α;A球由静止释放,摆到最低点时恰与B球发生正碰,碰撞后,A球把轻质指示针C推移到与竖直线夹角为β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸,用来记录B球的落点.B球飞行的水平距离为S.用图中所示各个物理量的符号表示碰撞前后A、B两球的动量,则A球碰前动量为
mA
| 2gL(1-cosα) |
mA
,如碰撞时动量守恒,应满足的关系式为:| 2gL(1-cosα) |
mA
=mA
+mBS
.
| 2gL(1-cosα) |
| 2gL(1-cosβ) |
|
mA
=mA
+mBS
.
.| 2gL(1-cosα) |
| 2gL(1-cosβ) |
|
 用如图所示装置来验证动量守恒定律.质量为mA的钢球A用细线悬挂于O点,质量为mB的钢球B放在离地面高度为H的小支柱N上,O点到A球球心的距离为L,使悬线在A球释放前伸直,且线与竖直线夹角为α,A球释放后摆到最低点时恰与B球正碰,碰撞后,A球把轻质指示针OC推移到与竖直线夹角β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸D,保持α角度不变,多次重复上述实验,白纸上记录到多个B球的落点.(已知当地的重力加速度为g)
用如图所示装置来验证动量守恒定律.质量为mA的钢球A用细线悬挂于O点,质量为mB的钢球B放在离地面高度为H的小支柱N上,O点到A球球心的距离为L,使悬线在A球释放前伸直,且线与竖直线夹角为α,A球释放后摆到最低点时恰与B球正碰,碰撞后,A球把轻质指示针OC推移到与竖直线夹角β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸D,保持α角度不变,多次重复上述实验,白纸上记录到多个B球的落点.(已知当地的重力加速度为g)(1)为验证两球碰撞过程动量守恒,应测出数值的物理量有S以及
mA、mB、α、β、H、L
mA、mB、α、β、H、L
.(用题中字母表示)(2)用测得的物理量表示碰撞前后A球、B球的动量:PA=
mA
| 2gL(1-cosα) |
mA
,PA′=| 2gL(1-cosα) |
mA
| 2gL(1-cosβ) |
mA
.PB=0,PB′=| 2gL(1-cosβ) |
mBS
|
mBS
.
|