题目内容
用如图所示装置来验证动量守恒定律，质量为m
B的钢球B放在小支柱N上，离地面高度为H；质量为m
A的钢球A用细线拴好悬挂于O点，当细线被拉直时O点到球心的距离为L，且细线与竖直线之间夹角为α；球A由静止释放，摆到最低点时恰与球B发生正碰，碰撞后，A球把轻质指示针C推移到与竖直夹角为β处，B球落到地面上，地面上铺有一张盖有复写纸的白纸D，用来记录球 B 的落点．
用图中所示各个物理量的符号表示碰撞前后两球A、B的动量（设两球A、B碰前的动量分别为p
A、p
B； 碰后动量分别为 P
A′、P
B′，则P
A=
，P
A′=
，P
B=
0
0
，P
B′=
．
分析：A球下摆过程机械能守恒，根据守恒定律列式求最低点速度；球A上摆过程机械能再次守恒，可求解碰撞后速度；碰撞后小球B做平抛运动，根据平抛运动的分位移公式求解碰撞后B球的速度，然后验证动量是否守恒即可．
解答：解：小球从A处下摆过程只有重力做功，机械能守恒，由机械能守恒定律得：
m
AgL（1-cosα）=
m
Av
A2-0，解得：v
A=
，则P
A=m
Av
A=m
A；
小球A与小球B碰撞后继续运动，在A碰后到达最左端过程中，机械能再次守恒，
由机械能守恒定律得：-m
AgL（1-cosβ）=0-
m
Av
A′
2，解得v
A′=
，
P
A′=m
Av
A′=m
A；
碰前小球B静止，则P
B=0；
碰撞后B球做平抛运动，水平方向：S=v
B′t，竖直方向H=
gt
2，
解得v
B′=S
，则碰后B球的动量P
B′=m
Bv
B′=m
BS
；
故答案为：m
A；m
A；0；m
BS
．
点评：本题解题的关键是要明确两小球的运动过程以及过程中机械能何时守恒，动量何时守恒．
练习册系列答案
相关题目
名校课堂系列答案
用如图所示装置来验证动量守恒定律，质量为mA的小钢球A用细线悬挂于O点，质量为mB的钢球B放在O点正下方离地面高度为H的小支柱N上，A球的悬线长度为L，使悬线在A球释放前伸直，且线与竖直线夹角为α，A球释放后摆到最低点时恰与B球正碰，碰撞后，A球把轻质指示针OC推移到与竖直线夹角β处，B球落到地面上，地面上铺有一张盖有复写纸的白纸D，保持α角度不变，多次重复上述实验，白纸上记录到多个B
用如图所示装置来验证动量守恒定律，质量为mB的钢球B放在小支柱N上，球心离地面高度为H；质量为mA的钢球A用细线拴好悬挂于O点，当细线被拉直时O点到球心的距离为L，且细线与竖直线之间夹角α；球A由静止释放，摆到最低点时恰与球B发生正碰，碰撞后，A球把轻质指示针C推移到与竖直夹角为β处，B球落到地面上，地面上铺有一张盖有复写纸的白纸D，用来记录球B的落点．
用如图所示装置来验证动量守恒定律，质量为mB的钢球B放在小支柱上，球心离地面高度为H；质量为mA的钢球A用细线栓好悬挂于O点，当细线被拉直时O点到球心的距离为L，且细线与竖直线之间夹角为α；A球由静止释放，摆到最低点时恰与B球发生正碰，碰撞后，A球把轻质指示针C推移到与竖直线夹角为β处，B球落到地面上，地面上铺有一张盖有复写纸的白纸，用来记录B球的落点．B球飞行的水平距离为S．
用如图所示装置来验证动量守恒定律．质量为mA的钢球A用细线悬挂于O点，质量为mB的钢球B放在离地面高度为H的小支柱N上，O点到A球球心的距离为L，使悬线在A球释放前伸直，且线与竖直线夹角为α，A球释放后摆到最低点时恰与B球正碰，碰撞后，A球把轻质指示针OC推移到与竖直线夹角β处，B球落到地面上，地面上铺有一张盖有复写纸的白纸D，保持α角度不变，多次重复上述实验，白纸上记录到多个B球的落点．（已知当地的重力加速度为g）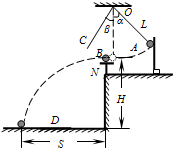
（1）有以下几个实验：