äãá¢áÖàï
 ÆûàÓë¥ùªòƒæ¯øûâÇîÕøÊÑ₤ê¢òĤÐÑ´ôèȘøòê¢öˆmBçá¡øú·BñéåÖÅÀøÏøªNèüȘú·ÅáâŠçÄûÌ¡ÔÑàöˆHÈ£øòê¢öˆmAçá¡øú·AÆûü¡üÔùˋ¤ûÅ■¿ØÆÖOçÐȘçÝü¡üÔÝ£âÙøÝòÝOçÐç§ú·ÅáçáƒÁâŠöˆLȘúØü¡üÔÆŠòºøÝüÔøÛ¥ð¥Å§úÎêÈ£ú·AÆèƒýø¿òëñéȘ¯Öç§æŸçëçÐòÝúÀÆŠú·BñÂèºí»é—Șé—æý¤µÈ˜Aú·¯îúÃøòø¡òƒíŠCëóØóç§ÆŠòºøݥŧúöˆÎôÇÎȘBú·ôðç§çÄûÌèüȘçÄûÌèüóäÆÅØ£íé¡úÆÅ¡ÇÅÇø§çá¯æø§DȘÆûâÇ¥úô¥ú·BçáôðçÐÈÛ
ÆûàÓë¥ùªòƒæ¯øûâÇîÕøÊÑ₤ê¢òĤÐÑ´ôèȘøòê¢öˆmBçá¡øú·BñéåÖÅÀøÏøªNèüȘú·ÅáâŠçÄûÌ¡ÔÑàöˆHÈ£øòê¢öˆmAçá¡øú·AÆûü¡üÔùˋ¤ûÅ■¿ØÆÖOçÐȘçÝü¡üÔÝ£âÙøÝòÝOçÐç§ú·ÅáçáƒÁâŠöˆLȘúØü¡üÔÆŠòºøÝüÔøÛ¥ð¥Å§úÎêÈ£ú·AÆèƒýø¿òëñéȘ¯Öç§æŸçëçÐòÝúÀÆŠú·BñÂèºí»é—Șé—æý¤µÈ˜Aú·¯îúÃøòø¡òƒíŠCëóØóç§ÆŠòºøݥŧúöˆÎôÇÎȘBú·ôðç§çÄûÌèüȘçÄûÌèüóäÆÅØ£íé¡úÆÅ¡ÇÅÇø§çá¯æø§DȘÆûâÇ¥úô¥ú·BçáôðçÐÈÛÈ´1ÈˋöˆêùÝÈøÊú·A¯îú·Bç₤°—¤µáÉ¥äŽü·ú¯¯ÖÑ₤ȘÆΡûôºæÐçá¿ÄüçòúmA
ǵÆÖ
ǵÆÖ
mBÈ´2ÈˋÆûë¥øÅùªòƒ¡¼¡—öÿâÚê¢çáñ«¤éÝÚòƒé—æýú¯¤µê§ú·AÀÂBçáÑ₤ê¢È´èÒê§ú·AÀÂBé—ú¯çáÑ₤ê¢ñøÝÞöˆPAÀÂPBȣ闤µÑ₤ê¢ñøÝÞöˆ
| P | Àð A |
| P | Àð B |
mA
| 2gl(1-cosÎê) |
mA
È£| 2gl(1-cosÎê) |
| P | Àð A |
mA
| 2gl(1-cosÎô) |
mA
È£PB=| 2gl(1-cosÎô) |
0
0
È£| P | Àð B |
mBS
|
mBS
ÈÛ
|
ñøö—Ȥȴ1Èˋ¡ªƒïÑ₤ê¢òĤФëáÉê¢òĤÐúµ°—é—¤µAú·çáùìÑàȘÇÆѽéÅÑü°—Aú·¥äŽü·ú¯¯ÖÑ₤Șê§ú·çáøòꢿÄüçÈÛ
È´2Èˋ¡ªƒï£ºÅçáÉòĤФëó§éæåùÑ₤çá¿Ìôèúµ°—é—ú¯¤ëé—¤µÅÀú·çáùìÑàȘÇÆѽçû°—Ñ₤ê¢çáǵÅÀÈÛ
È´2Èˋ¡ªƒï£ºÅçáÉòĤФëó§éæåùÑ₤çá¿Ìôèúµ°—é—ú¯¤ëé—¤µÅÀú·çáùìÑàȘÇÆѽçû°—Ñ₤ê¢çáǵÅÀÈÛ
§ãÇÞȤ§ãȤȴ1ÈˋåÖÅÀú·é—æý¿»°äøÅùÛó§ñ§ü·Ñ₤ê¢òĤÐÑ´ôè¿òÆÅmAv0=mAv1+mBv2
åÖé—æý¿»°äøÅÑ₤áÉòĤпòÆÅ
mAv02=
mAv12+
mBv22ÈÛ
§ãçûv1=
v0ÈÛ
؈闤µàŠèðÅÀú·çáùìÑàv1ȃ0Ș¥ÇmA-mBȃ0ȘmAȃmBÈÛ
È´2Èˋ¡ªƒï£ºÅçáÉòĤÐÑ´ôèçûȘmAgLÈ´1-cosÎêÈˋ=
mAv02Ș§ãçûv0=
ȘùªØåPA=mA
ÈÛ
¡ªƒï£ºÅçáÉòĤÐÑ´ôèçûȘmAgL(1-cosÎô)´T
mAv12Ș§ãçûv1=
ȘùªØåPAÀð=mA
ÈÛ
Bú·é—æýú¯ƒýø¿È˜ùªØåPB=0ÈÛ
¡ªƒïH=
gt2çûȘt=
Șå·vB=
=S
ÈÛ
ùªØåPBÀð=mBS
ÈÛ
¿òÇÞ¯¡öˆÈ¤È´1ÈˋǵÆÖ È´2ÈˋmA
ȘmA
Ș0 mBS
åÖé—æý¿»°äøÅÑ₤áÉòĤпòÆÅ
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
§ãçûv1=
| mA-mB |
| mA+mB |
؈闤µàŠèðÅÀú·çáùìÑàv1ȃ0Ș¥ÇmA-mBȃ0ȘmAȃmBÈÛ
È´2Èˋ¡ªƒï£ºÅçáÉòĤÐÑ´ôèçûȘmAgLÈ´1-cosÎêÈˋ=
| 1 |
| 2 |
| 2gL(1-cosÎê) |
| 2gl(1-cosÎê) |
¡ªƒï£ºÅçáÉòĤÐÑ´ôèçûȘmAgL(1-cosÎô)´T
| 1 |
| 2 |
| 2gL(1-cosÎô) |
| 2gl(1-cosÎô) |
Bú·é—æýú¯ƒýø¿È˜ùªØåPB=0ÈÛ
¡ªƒïH=
| 1 |
| 2 |
|
| S |
| t |
|
ùªØåPBÀð=mBS
|
¿òÇÞ¯¡öˆÈ¤È´1ÈˋǵÆÖ È´2ÈˋmA
| 2gl(1-cosÎê) |
| 2gl(1-cosÎô) |
|
çÐóâȤ݃ä㢥ýÕêùÑ₤ê¢òĤÐÑ´ôè¤ë£ºÅçáÉòĤÐÑ´ôèçáæܤüåùÆûȘøˆçâAú·ÆŠBé—¤µÈ˜Aú·¥äŽü·ú¯åùÑ₤ȘAÀÂBê§ú·çáøòꢿÄüçÈÛ

êñü¯ýÃüçêÅÇÞ¯¡
 ¢óîÏòçîÕ£ŸÑ₤ýÃüçêÅÇÞ¯¡
¢óîÏòçîÕ£ŸÑ₤ýÃüçêÅÇÞ¯¡
üÁ¿Ääãá¢
 ÆûàÓë¥ùªòƒæ¯øûâÇîÕøÊÑ₤ê¢òĤÐÑ´ôèȘøòê¢öˆmAçáÅÀ¡øú·AÆûü¡üÔÅ■¿ØÆÖOçÐȘøòê¢öˆmBçá¡øú·BñéåÖOçÐí»üôñ§âŠçÄûÌ¡ÔÑàöˆHçáÅÀøÏøªNèüȘAú·çáÅ■üÔ°ÊÑàöˆLȘò¿Å■üÔåÖAú·òëñéú¯èšøÝȘúØüÔÆŠòºøÝüԥŧúöˆÎêȘAú·òëñ餵¯Öç§æŸçëçÐòÝúÀÆŠBú·í»é—Șé—æý¤µÈ˜Aú·¯îúÃøòø¡òƒíŠOCëóØóç§ÆŠòºøÝüԥŧúÎôÇÎȘBú·ôðç§çÄûÌèüȘçÄûÌèüóäÆÅØ£íé¡úÆÅ¡ÇÅÇø§çá¯æø§DȘÝÈ°øÎê§úÑàý£ÝðȘÑÁÇöøÄ¡Çèüò—òçîÕȘ¯æø§èü¥úô¥ç§ÑÁ¡—B
ÆûàÓë¥ùªòƒæ¯øûâÇîÕøÊÑ₤ê¢òĤÐÑ´ôèȘøòê¢öˆmAçáÅÀ¡øú·AÆûü¡üÔÅ■¿ØÆÖOçÐȘøòê¢öˆmBçá¡øú·BñéåÖOçÐí»üôñ§âŠçÄûÌ¡ÔÑàöˆHçáÅÀøÏøªNèüȘAú·çáÅ■üÔ°ÊÑàöˆLȘò¿Å■üÔåÖAú·òëñéú¯èšøÝȘúØüÔÆŠòºøÝüԥŧúöˆÎêȘAú·òëñ餵¯Öç§æŸçëçÐòÝúÀÆŠBú·í»é—Șé—æý¤µÈ˜Aú·¯îúÃøòø¡òƒíŠOCëóØóç§ÆŠòºøÝüԥŧúÎôÇÎȘBú·ôðç§çÄûÌèüȘçÄûÌèüóäÆÅØ£íé¡úÆÅ¡ÇÅÇø§çá¯æø§DȘÝÈ°øÎê§úÑàý£ÝðȘÑÁÇöøÄ¡Çèüò—òçîÕȘ¯æø§èü¥úô¥ç§ÑÁ¡—B ÆûàÓë¥ùªòƒæ¯øûâÇîÕøÊÑ₤ê¢òĤÐÑ´ôèȘøòê¢öˆmBçá¡øú·BñéåÖÅÀøÏøªèüȘú·ÅáâŠçÄûÌ¡ÔÑàöˆHÈ£øòê¢öˆmAçá¡øú·AÆûü¡üÔù´¤ûÅ■¿ØÆÖOçÐȘçÝü¡üÔÝ£âÙøÝòÝOçÐç§ú·ÅáçáƒÁâŠöˆLȘúØü¡üÔÆŠòºøÝüÔøÛ¥ð¥Å§úöˆÎêÈ£Aú·Æèƒýø¿òëñéȘ¯Öç§æŸçëçÐòÝúÀÆŠBú·ñÂèºí»é—Șé—æý¤µÈ˜Aú·¯îúÃøòø¡òƒíŠCëóØóç§ÆŠòºøÝüԥŧúöˆÎôÇÎȘBú·ôðç§çÄûÌèüȘçÄûÌèüóäÆÅØ£íé¡úÆÅ¡ÇÅÇø§çá¯æø§È˜ÆûâÇ¥úô¥Bú·çáôðçÐÈÛBú·ñèÅÅçáùÛó§ƒÁâŠöˆSÈÛ
ÆûàÓë¥ùªòƒæ¯øûâÇîÕøÊÑ₤ê¢òĤÐÑ´ôèȘøòê¢öˆmBçá¡øú·BñéåÖÅÀøÏøªèüȘú·ÅáâŠçÄûÌ¡ÔÑàöˆHÈ£øòê¢öˆmAçá¡øú·AÆûü¡üÔù´¤ûÅ■¿ØÆÖOçÐȘçÝü¡üÔÝ£âÙøÝòÝOçÐç§ú·ÅáçáƒÁâŠöˆLȘúØü¡üÔÆŠòºøÝüÔøÛ¥ð¥Å§úöˆÎêÈ£Aú·Æèƒýø¿òëñéȘ¯Öç§æŸçëçÐòÝúÀÆŠBú·ñÂèºí»é—Șé—æý¤µÈ˜Aú·¯îúÃøòø¡òƒíŠCëóØóç§ÆŠòºøÝüԥŧúöˆÎôÇÎȘBú·ôðç§çÄûÌèüȘçÄûÌèüóäÆÅØ£íé¡úÆÅ¡ÇÅÇø§çá¯æø§È˜ÆûâÇ¥úô¥Bú·çáôðçÐÈÛBú·ñèÅÅçáùÛó§ƒÁâŠöˆSÈÛ ÆûàÓë¥ùªòƒæ¯øûâÇîÕøÊÑ₤ê¢òĤÐÑ´ôèÈÛøòê¢öˆmAçá¡øú·AÆûü¡üÔÅ■¿ØÆÖOçÐȘøòê¢öˆmBçá¡øú·BñéåÖâŠçÄûÌ¡ÔÑàöˆHçáÅÀøÏøªNèüȘOçÐç§Aú·ú·ÅáçáƒÁâŠöˆLȘò¿Å■üÔåÖAú·òëñéú¯èšøÝȘúØüÔÆŠòºøÝüԥŧúöˆÎêȘAú·òëñ餵¯Öç§æŸçëçÐòÝúÀÆŠBú·í»é—Șé—æý¤µÈ˜Aú·¯îúÃøòø¡òƒíŠOCëóØóç§ÆŠòºøÝüԥŧúÎôÇÎȘBú·ôðç§çÄûÌèüȘçÄûÌèüóäÆÅØ£íé¡úÆÅ¡ÇÅÇø§çá¯æø§DȘÝÈ°øÎê§úÑàý£ÝðȘÑÁÇöøÄ¡Çèüò—òçîÕȘ¯æø§èü¥úô¥ç§ÑÁ¡—Bú·çáôðçÐÈÛÈ´ØîøˆçÝçÄçáøÄêÎ¥ÆùìÑàöˆgÈˋ
ÆûàÓë¥ùªòƒæ¯øûâÇîÕøÊÑ₤ê¢òĤÐÑ´ôèÈÛøòê¢öˆmAçá¡øú·AÆûü¡üÔÅ■¿ØÆÖOçÐȘøòê¢öˆmBçá¡øú·BñéåÖâŠçÄûÌ¡ÔÑàöˆHçáÅÀøÏøªNèüȘOçÐç§Aú·ú·ÅáçáƒÁâŠöˆLȘò¿Å■üÔåÖAú·òëñéú¯èšøÝȘúØüÔÆŠòºøÝüԥŧúöˆÎêȘAú·òëñ餵¯Öç§æŸçëçÐòÝúÀÆŠBú·í»é—Șé—æý¤µÈ˜Aú·¯îúÃøòø¡òƒíŠOCëóØóç§ÆŠòºøÝüԥŧúÎôÇÎȘBú·ôðç§çÄûÌèüȘçÄûÌèüóäÆÅØ£íé¡úÆÅ¡ÇÅÇø§çá¯æø§DȘÝÈ°øÎê§úÑàý£ÝðȘÑÁÇöøÄ¡Çèüò—òçîÕȘ¯æø§èü¥úô¥ç§ÑÁ¡—Bú·çáôðçÐÈÛÈ´ØîøˆçÝçÄçáøÄêÎ¥ÆùìÑàöˆgÈˋ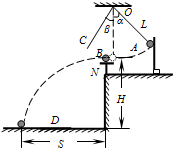 È´1ÈˋÆÅØåüô¥¡¡—òçîÕȤ
È´1ÈˋÆÅØåüô¥¡¡—òçîÕȤ