安徽省蚌埠市2009届高三年级第一次教学质量检查考试
数 学(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间为120分钟
第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的,)
1、已知全集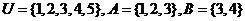 ,则
,则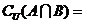
A、{3} B、{4,5} C、{1,2,4,5} D、{1,2,3,4}
2、已知函数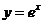 的图像与函数
的图像与函数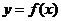 的图像关于直线
的图像关于直线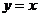
对称,则
A、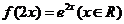 B、
B、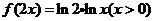
C、 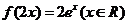 D、
D、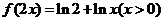
3、若函数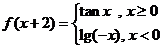 ,则
,则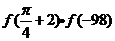 等于
等于
A、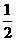 B、
B、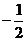 C、2 D、
C、2 D、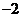
4、已知直线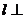 平面
平面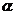 ,直线
,直线 平面
平面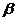 ,给出下列命题:①
,给出下列命题:①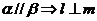 ;②
;②
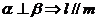 ;③
;③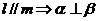 ;④
;④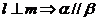 ,其中正确命题的序号是
,其中正确命题的序号是
A、①②③ B、②③④ C、②④ D、①③
5、已知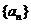 是等比数列,
是等比数列,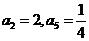 ,则
,则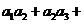 …
…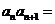
A、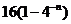 B、
B、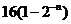 C、
C、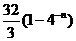 D、
D、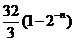
6、设命题p:命题“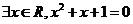 ”的否定是“
”的否定是“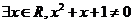 ”;命题
”;命题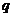 :
:
“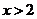 ”是“
”是“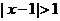 ”的充分不必要条件,则
”的充分不必要条件,则
A、“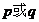 ”为真 B、“
”为真 B、“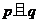 ”为真 C、
”为真 C、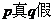 D、
D、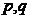 均为假命题
均为假命题
7、如果平面的一条斜线和它在这个平面上的射影的方向向量分别是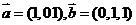 那么这条斜线与平面所成的角是
那么这条斜线与平面所成的角是
A、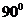 B、
B、 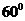 C、
C、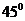 D、
D、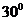
8、已知函数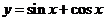 ,给出以下四个命题,其中为真命题的是
,给出以下四个命题,其中为真命题的是
A、若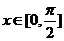 ,则
,则 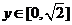 B、在区间
B、在区间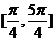 上是增函数
上是增函数
C、直线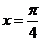 是函数图象的一条对称轴
是函数图象的一条对称轴
D、函数的图象可由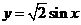 的图象向右平移
的图象向右平移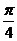 个单位得到
个单位得到
9、椭圆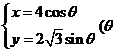 为参数)的长轴为
为参数)的长轴为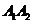 ,短轴为
,短轴为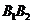 ,将椭圆沿y轴折成一个二面角,使得
,将椭圆沿y轴折成一个二面角,使得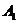 点在平面
点在平面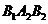 上的射影恰好为椭圆的右焦点,则该二面角的大小为
上的射影恰好为椭圆的右焦点,则该二面角的大小为
A、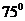 B、
B、 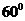 C、
C、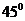 D、
D、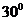
10、已知图中一组函数图象,它们分别与其后所列的一个现实情境相匹配:
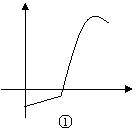 |
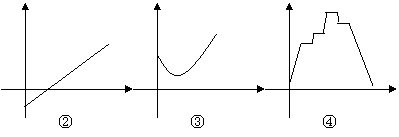 |
情境A:一份30分钟前从冰箱里取出来,然后被防到微波炉里加热,最后放到餐桌上的食物的温度(将0时刻确定为食物从冰箱里被取出来的那一刻)
情境B:一个1970年生产的留声机从它刚开始的售价到现在的价值(它被一个爱好者收藏,并且被保存的很好);
情境C:从你刚开始防水洗澡,到你洗完后把它排掉这段时间浴缸里水的高度;
情境D:根据乘客人数,每辆公交车一趟营运的利润。
其中与情境A、B、、C、D对应的图象正确的序号是
 11、将“新、安、徽”填入3×3方格中,要求每行、每列都每有重复文字,如右图是一种填法,则不同的填写方法有
11、将“新、安、徽”填入3×3方格中,要求每行、每列都每有重复文字,如右图是一种填法,则不同的填写方法有
A、6种 B、12种 C、24种 D、48种
12、如图是一个由三根细棒PA、PB、PC组成的支架,
三根细棒PA、PB、PC两两所成的角都为600,一个半
径为1的小球放在支架上,则球心O到点P 的距离是
A、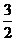 B、
B、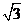 D、
D、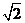
二、填空题:本大题共4个小题,每小题4分,共16分,请将答案直接填在题中横线上。
13、极坐标系中,曲线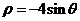 和
和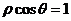 相交于点A、B则线段AB的长度为_____
相交于点A、B则线段AB的长度为_____
14、二项式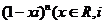 为虚数单位)的展开式中含
为虚数单位)的展开式中含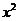 项的系数等于―28,则n
项的系数等于―28,则n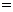 _____.
_____.
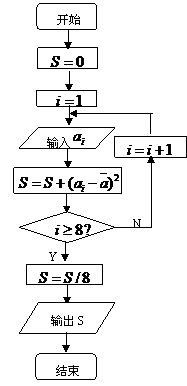 15、在平面直角坐标系中,不等式组
15、在平面直角坐标系中,不等式组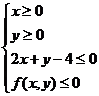 所表示的平面区域的面积是
所表示的平面区域的面积是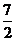 ,请写出满足条件的一个不等式
,请写出满足条件的一个不等式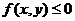 ;______________。
;______________。
16、对一个作直线运动的质点的运动过程观
测了8次,得到如下表所示的数据:
观测次数
1
2
3
4
5
6
7
8
观测数据
40
41
43
43
44
46
47
48
在上述统计数据的分析中,一部分计算机如图所示的算法
流程图(其中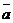 是这8个数据的平均数),则输出的S的值
是这8个数据的平均数),则输出的S的值
是____________________。
、证明过程和演算步骤。
三、解答题:本大题共6个小题,共74分,解答须写出说明
17、(本小题12分)设△ABC的内角A、B、C所对的边长
分别为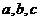 ,若
,若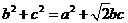
(1)求A的大小;
(2)求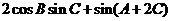 的值。
的值。
周销售量(单位:吨)
2
3
4
频数
20
50
30
18、(本小题12分)某批发市场对某种商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
(1)根据上面的统计结果,求周销售量分别为2吨,3吨和4吨的频率;
(2)已知每吨该商品的销售利润为2千元,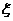 表示该商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求
表示该商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求 的分布列和均值(数学期望)
的分布列和均值(数学期望)
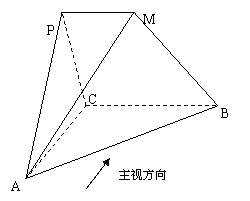 19、(本小题12分)如图所示几何体中,平面PAC⊥平面ABC,批PM//BC,PA=PC,AC=1,BC=2PM=2,AB=
19、(本小题12分)如图所示几何体中,平面PAC⊥平面ABC,批PM//BC,PA=PC,AC=1,BC=2PM=2,AB=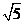 ,若该几何体左试图(侧视图)的面积为
,若该几何体左试图(侧视图)的面积为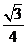
(1)求证:PA⊥BC;
(2)画出该几何体的主试图并求其面积S;
(3)求多面体PMABC的体积V
20、(本小题12分)设函数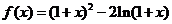
(1)若在定义域内存在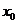 使得不等式
使得不等式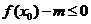 能成立,求实数m的最小值;
能成立,求实数m的最小值;
(2)若函数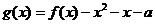 在区间[0,2]上恰有两个不同的零点,求实数
在区间[0,2]上恰有两个不同的零点,求实数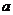 的取值范围。
的取值范围。
21、(本小题12分)已知曲线C上任意一点P到直线x=1与点F(―1,0)的距离相等。
(1)求曲线C的方程;
(2)设直线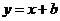 与曲线C交于点A、B,问在直线
与曲线C交于点A、B,问在直线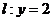 上是否存在于b无关的定点M,使得直线MA,MB关于直线
上是否存在于b无关的定点M,使得直线MA,MB关于直线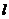 对称,若存在,求出点M的坐标,若不存在,请说明理由。
对称,若存在,求出点M的坐标,若不存在,请说明理由。
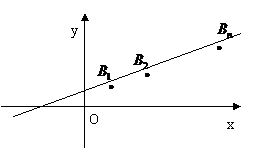 22、(本小题14分)已知点
22、(本小题14分)已知点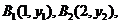 …,
…,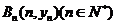 在直线
在直线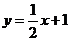 上,点
上,点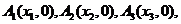 …,
…, 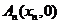 顺次为x轴上的点,其中
顺次为x轴上的点,其中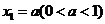 ,对任意n
,对任意n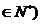 ,点
,点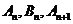 构成以
构成以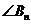 为顶角的等腰三角形,设△
为顶角的等腰三角形,设△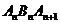 的面积为
的面积为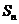
(1)证明:数列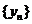 是等差数列;
是等差数列;
(2)求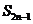 ;(用a和n的代数式表示);
;(用a和n的代数式表示);
(3)设数列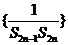 的前n项和为
的前n项和为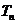 ,
,
判断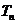 与
与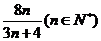 的大小,并证明你的结论。
的大小,并证明你的结论。
安徽省蚌埠市2009届高三年级第一次教学质量检查考试
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
C
D
C
A
B
C
B
D
B
C
二、填空题:
13、 14、8 15、
14、8 15、 等; 16、7
等; 16、7
三、解答题
17、(1)由余弦定理: 又
又
∴ ∴
∴
(2)∵A+B+C= ∴
∴
∴
18、(1)周销售量为2吨,3吨,4吨的频率分别为0.2,0.5,和0.3。
(2) 可能的值为8,10,12,14,16
可能的值为8,10,12,14,16






8
10
12
14
16
P
0.04
0.2
0.37
0.3
0.09
则 的分布列为
的分布列为
∴ (千元)
(千元)
19、(1)AC=1,BC=2 ,AB= ,∴
,∴ ∴AC
∴AC
又 平面PAC 平面ABC,平面PAC
平面ABC,平面PAC 平面ABC=AC,∴BC
平面ABC=AC,∴BC 平面PAC
平面PAC
又∵PA 平面APC ∴
平面APC ∴
 (2)该几何体的主试图如下:
(2)该几何体的主试图如下:
几何体主试图的面积为
 ∴
∴ ∴
∴
(3)取PC 的中点N,连接AN,由△PAC是边长为1的正三角形,可知
由(1)BC 平面PAC,可知
平面PAC,可知 ∴
∴ 平面PCBM
平面PCBM
∴
20、(1)要使得不等式 能成立,只需
能成立,只需
 ∴
∴
∴ ,故实数m的最小值为1
,故实数m的最小值为1
(2)由 得
得
令 ∵
∵ ,列表如下:
,列表如下:
x
0
(0,1)
1
(1,2)
2


0


1
减函数

增函数
3-2ln3
∴
21、(1)曲线C的方程为
(2) ,存在点M(―1,2)满足题意
,存在点M(―1,2)满足题意
22、(1)由于点B1(1,y1),B2(2,y2),…,Bn(n,yn)( )在直线
)在直线 上
上
则 因此
因此 ,所以
,所以 是等差数列
是等差数列
(2)由已知有 得
得 同理
同理 
∴
∴

∴
(3)由(2)得 ,则
,则

∴
∴
∴
由于 而
而
则
 ,从而
,从而
同理: ……
…… 
以上 个不等式相加得:
个不等式相加得:
即 ,从而
,从而
