摘要:观测数据4041434344464748在上述统计数据的分析中.一部分计算机如图所示的算法
网址:http://m.1010jiajiao.com/timu_id_303274[举报]
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
C
D
C
A
B
C
B
D
B
C
二、填空题:
13、 14、8 15、
14、8 15、 等; 16、7
等; 16、7
三、解答题
17、(1)由余弦定理: 又
又
∴ ∴
∴
(2)∵A+B+C= ∴
∴
∴
18、(1)周销售量为2吨,3吨,4吨的频率分别为0.2,0.5,和0.3。
(2) 可能的值为8,10,12,14,16
可能的值为8,10,12,14,16






8
10
12
14
16
P
0.04
0.2
0.37
0.3
0.09
则 的分布列为
的分布列为
∴ (千元)
(千元)
19、(1)AC=1,BC=2 ,AB= ,∴
,∴ ∴AC
∴AC
又 平面PAC 平面ABC,平面PAC
平面ABC,平面PAC 平面ABC=AC,∴BC
平面ABC=AC,∴BC 平面PAC
平面PAC
又∵PA 平面APC ∴
平面APC ∴
 (2)该几何体的主试图如下:
(2)该几何体的主试图如下:
几何体主试图的面积为
 ∴
∴ ∴
∴
(3)取PC 的中点N,连接AN,由△PAC是边长为1的正三角形,可知
由(1)BC 平面PAC,可知
平面PAC,可知 ∴
∴ 平面PCBM
平面PCBM
∴
20、(1)要使得不等式 能成立,只需
能成立,只需
 ∴
∴
∴ ,故实数m的最小值为1
,故实数m的最小值为1
(2)由 得
得
令 ∵
∵ ,列表如下:
,列表如下:
x
0
(0,1)
1
(1,2)
2


0


1
减函数

增函数
3-2ln3
∴
21、(1)曲线C的方程为
(2) ,存在点M(―1,2)满足题意
,存在点M(―1,2)满足题意
22、(1)由于点B1(1,y1),B2(2,y2),…,Bn(n,yn)( )在直线
)在直线 上
上
则 因此
因此 ,所以
,所以 是等差数列
是等差数列
(2)由已知有 得
得 同理
同理 
∴
∴

∴
(3)由(2)得 ,则
,则

∴
∴
∴
由于 而
而
则
 ,从而
,从而
同理: ……
…… 
以上 个不等式相加得:
个不等式相加得:
即 ,从而
,从而

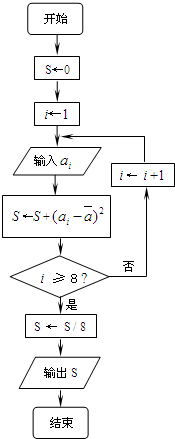 对一个作直线运动的质点的运动过程观测了8次,第i次观测得到的数据为ai,具体如下表所示:
对一个作直线运动的质点的运动过程观测了8次,第i次观测得到的数据为ai,具体如下表所示:| 观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 观测数据ai | 40 | 41 | 43 | 43 | 44 | 46 | 47 | 48 |
. |
| a |
为了考察两个变量x和y之间的线性相关性,甲、乙两位同学各自独立地做10次和15次试验,并且利用线性回归方法,求得回归直线分别为l1和l2.已知两个人在试验中发现对变量x的观测数据的平均数都为s,对变量y的观测数据的平均数都为t,则下列说法正确的是( )
查看习题详情和答案>>
已知两个变量x与y之间具有线性相关关系,5次试验的观测数据如下:
那么变量y关于x的回归直线方程只可能是( )
| x | 100 | 120 | 140 | 160 | 180 |
| y | 45 | 54 | 62 | 75 | 92 |
A、
| ||
B、
| ||
C、
| ||
D、
|


