温州中学
高二数学试卷(文科)
一、选择题(每小题4分,共40分)
1.已知全集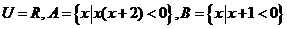 ,则下列表示图中阴影部分的集合为( )
,则下列表示图中阴影部分的集合为( )
 A.
A.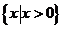 B.
B.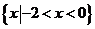
C.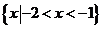 D.
D.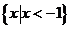
2.复数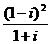 对应的点位于 ( )
对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.若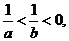 则下列结论不正确的是( )
则下列结论不正确的是( )
A.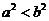 B.
B.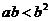 C.
C.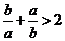 D.
D.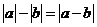
4.人寿保险的广告词为:“幸福的人们都拥有”,初听起来,这似乎只是普通的赞美说词,然
而他的实际效果大哩,原来这句话的等价命题是( )
A.不拥有的人们不一定幸福 B.不拥有的人们可能幸福
C.拥有的人们不一定幸福 D.不拥有的人们不幸福
5.条件p: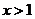 ,
,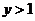 ,条件q:
,条件q: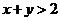 ,
,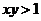 ,则条件p是条件q的 ( )
,则条件p是条件q的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.即不充分也不必要条件
6.已知函数f (x)的导数为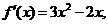 且图象过点(1,2),则函数f (x)的极大值为( )
且图象过点(1,2),则函数f (x)的极大值为( )
A.0 B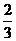
7.用反证法证明命题:“三角形的内角中至少有一个不大于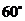 ”时,反设正确的是( )
”时,反设正确的是( )
A.假设三内角都不大于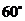 B.假设三内角都大于
B.假设三内角都大于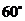
C.假设三内角至多有一个大于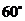 D.假设三内角至多有两个大于
D.假设三内角至多有两个大于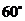
8.已知m ,
n 是直线, 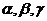 是平面,给出下列命题:
是平面,给出下列命题:
⑴若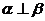 ,
, 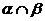 =m
, m
=m
, m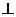 n,
则n
n,
则n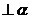 或n
或n ;
;
⑵若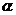 ∥
∥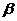 ,
,  =m
,
=m
, 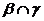 =n,
则m∥n;
=n,
则m∥n;
⑶若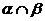 =m, n∥m
, 则n∥
=m, n∥m
, 则n∥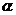 且n∥
且n∥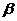 ;
;
⑷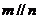 ,则m 、 n与
,则m 、 n与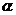 所成的角相等.
所成的角相等.
其中正确的命题序号为( )
A.⑴与⑵ B.⑵与⑷ C.⑶与⑷ D.⑴与⑶
9.函数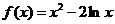 的单调减区间是( )
的单调减区间是( )
A.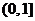 B.
B.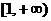 C.
C.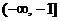 及
及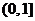 D.
D.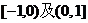
10.过ㄓABC的重心G任作一条直线EF,AD⊥EF于D,BE⊥EF于E,CF⊥EF于F,则向量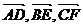 之间正确的关系是( )
之间正确的关系是( )
A. 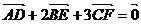 B.
B.
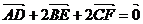
C. 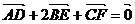 D.
D.

二、填空题(每小题4分,共16分)
11.复数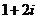 的虚部为 .
的虚部为 .
12.若函数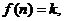 其中
其中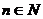 ,
,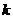 是
是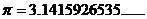 的小数点后第n位数字,例
的小数点后第n位数字,例
如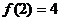 ,则
,则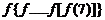 (共
(共
13.若函数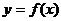 在(0,2)上是增函数,且函数的图象关于直线
在(0,2)上是增函数,且函数的图象关于直线 对称,则
对称,则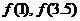 的大小关系是
.
的大小关系是
.
14.已知命题:平面上一矩形ABCD的对角线AC与边AB和AD所成角分别为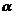 ?
?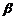 ,
,
则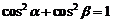 。若把它推广到空间长方体
。若把它推广到空间长方体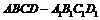 中,对角线
中,对角线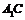 与平面
与平面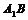 、
、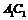 、
、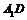 所成的角分别为
所成的角分别为 、
、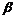 、
、 ,则
.
,则
.
三、解答题(15、16小题每题10分,17、18小题每题12分,共44分)
15.已知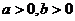 ,求证:
,求证: .
.
16.如图:D、E分别是正三棱柱ABC-A1B
(1)求证:A1E∥平面BDC1.
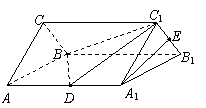 (2)求BD与平面CC1B1B所成角的正弦值.
(2)求BD与平面CC1B1B所成角的正弦值.
17.若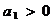 ,
,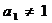 ,
,
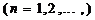
(1)求证: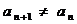 ;
;
(2)令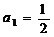 ,写出
,写出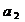 、
、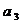 、
、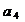 、
、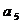 的值,观察并归纳出这个数列的通项公式
的值,观察并归纳出这个数列的通项公式 ;
;
(3)证明:存在不等于零的常数p,使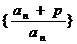 是等比数列,并求出公比q的值.
是等比数列,并求出公比q的值.
18.已知函数f (x) = x (1 +x)2.
(1)求实数a,b的值,使函数在区间[a,b]上的值域也为[a,b];
(2)设函数g (x) = kx -2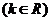 ,
, 在区间
在区间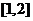 上恒成立,求k的取值范围.
上恒成立,求k的取值范围.
温州中学
高二数学(文科)答案
题号
1
2
3
4
5
6
7
8
9
10
答案
C
C
D
D
A
B
A
B
A
D
二、填空题(每小题4分,共16分)
11. 2 ; 12. 1 ;
13.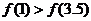 ;
;
14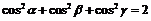 ,
,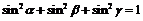 .
.
三、解答题
15. 证明: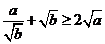
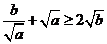
∴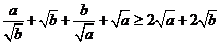
∴
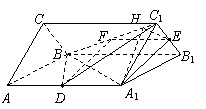 16.⑴证明:在线段BC1上取中点F,连结EF、DF
16.⑴证明:在线段BC1上取中点F,连结EF、DF
则由题意得EF∥DA1,且EF=DA1,
∴四边形EFDA1是平行四边形
∴A1E∥FD,又A1E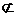 平面BDC1,FD
平面BDC1,FD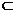 平面BDC1
平面BDC1
∴A1E∥平面BDC1
⑵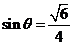
17.解:(1)采用反证法. 若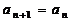 ,即
,即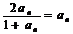 , 解得
, 解得 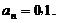
从而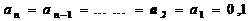 与题设
与题设 ,
,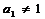 相矛盾,
相矛盾,
故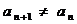 成立.
成立.
(2) 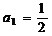 、
、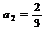 、
、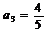 、
、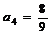 、
、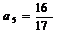 ,
, 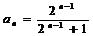 .
.
(3)因为 又
又 ,
,
所以 ,
,
因为上式是关于变量 的恒等式,故可解得
的恒等式,故可解得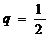 、
、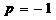 .
.
18. 解(1)由题意知, ,a,b即为方程f (x) = x的解,即 x (1 + x)2 = x,解得x1 = 0,x2 = ? 2.当?2≤x≤0时,检验知符合题意.∴a = ?2,b = 0.
,a,b即为方程f (x) = x的解,即 x (1 + x)2 = x,解得x1 = 0,x2 = ? 2.当?2≤x≤0时,检验知符合题意.∴a = ?2,b = 0.
(2)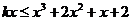 在区间
在区间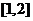 上恒成立
上恒成立
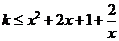 在区间
在区间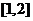 上恒成立
上恒成立
令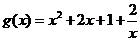 则
则
∴ ∴
∴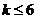 .
.