摘要：= kx -2.在区间上恒成立.求k的取值范围. 温州中学2008学年第二学期期中考试高二数学答案题号12345678910答案CCDDABABAD

网址：http://m.1010jiajiao.com/timu_id_265866[举报]

设二次函数f(x)＝ax²＋bx＋c的图象过点(0，1)和(1，4)，且对于任意的实数x，不等式f(x)≥4x恒成立．

(1)求函数f(x)的表达式；

(2)设g(x)＝kx＋1，若F(x)＝log₂[g(x)－f(x)]在区间[1，2]上是增函数，求实数k的取值范围．

已知函数g（x）=ax²-2ax+1+b（a＞0），在区间[2，3]上有最大值4，最小值1，设 $数学公式$ ．
（Ⅰ）求a、b的值；
（Ⅱ）若不等式f（x）-kx≥0在x∈（0，+∞）时恒成立，求实数k的取值范围；
（Ⅲ）方程 $数学公式$ 有三个不同的实数解，求实数k的取值范围．

(1)用x₀、f(x₀)、f′(x₀)表示m;

(2)证明当x₀∈(0,+∞)时,g(x)≥f(x);

(3)若关于x的不等式x²+1≥ax+b≥在上恒成立,其中a、b为实数，求b的取值范围及a与b 所满足的关系.

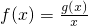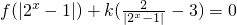已知函数g（x）=ax2-2ax+1+b（a＞0），在区间[2，3]上有最大值4，最小值1，设．（Ⅰ）求a、b的值；（Ⅱ）若不等式f（x）-kx≥0在x∈（0，+∞）时恒成立，求实数k的取值范围；（Ⅲ）方程有三个不同的实数解，求实数k的取值范围．