摘要:(3)证明:存在不等于零的常数p.使是等比数列.并求出公比q的值.
网址:http://m.1010jiajiao.com/timu_id_265864[举报]
已知A1(x1,y1),A2(x2,y2),…,An(xn,yn)是直线l:y=kx+b上的n个不同的点(n∈N*,k、b均为非零常数),其中数列{xn}为等差数列.
(1)求证:数列{yn}是等差数列;
(2)若点P是直线l上一点,且
=a1
+a2
,求证:a1+a2=1;
(3)设a1+a2+…+an=1,且当i+j=n+1时,恒有ai=aj(i和j都是不大于n的正整数,且i≠j).试探索:在直线l上是否存在这样的点P,使得
=a1
+a2
+…+an
成立?请说明你的理由.
查看习题详情和答案>>
(1)求证:数列{yn}是等差数列;
(2)若点P是直线l上一点,且
| OP |
| OA1 |
| OA2 |
(3)设a1+a2+…+an=1,且当i+j=n+1时,恒有ai=aj(i和j都是不大于n的正整数,且i≠j).试探索:在直线l上是否存在这样的点P,使得
| OP |
| OA1 |
| OA2 |
| OAn |
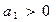 、
、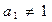 ,
,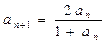
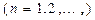
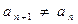 ;
;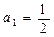 ,写出
,写出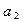 、
、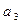 、
、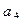 、
、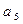 的值,观察并归纳出这个数列的通项公式
的值,观察并归纳出这个数列的通项公式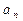 ;
;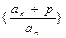 是等比数列,并求出公比q的值.
是等比数列,并求出公比q的值.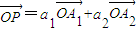 ,求证:a1+a2=1;
,求证:a1+a2=1;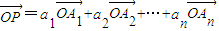 成立?请说明你的理由.
成立?请说明你的理由. (n=1,2,…)
(n=1,2,…) ,写出a2、a3、a4、a5的值,观察并归纳出这个数列的通项公式an;
,写出a2、a3、a4、a5的值,观察并归纳出这个数列的通项公式an; 是等比数列,并求出公比q的值.
是等比数列,并求出公比q的值.