2009年云南省曲靖一中高考冲刺卷理科数学(四)

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只
有一项是符合题目要求的.
1.设全集 ,则
,则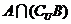 是
是
A.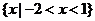 B.
B.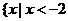 或
或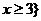

C. D.
D.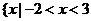 且
且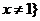

2.己知复数 满足
满足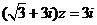 ,则
,则 等于
等于
A.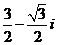 B.
B.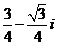 C.
C. D.
D.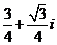

3.设等差数列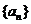 的前
的前 项和为
项和为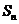 ,若
,若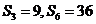 ,则
,则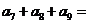

A.63 B.
4.设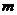 、
、 是不同的直线,
是不同的直线,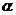 、
、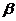 、
、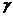 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
① 若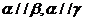 ,则
,则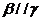 ② 若
② 若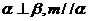 ,则
,则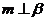

③ 若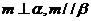 ,则
,则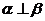 ④ 若
④ 若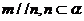 ,则
,则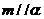

其中真命题的序号是
A.①④ B.②③ C.②④ D.①③
5.已知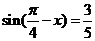 ,则
,则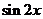 的值为
的值为
A.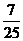 B.
B.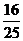 C.
C. D.
D.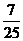

6.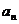 是
是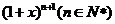 的展开式中含
的展开式中含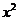 的项的系数,则
的项的系数,则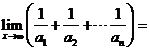

A.1 B.2 C.3 D.4
7.设双曲线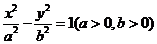 的离心率为
的离心率为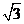 ,且它的一条准线与抛物线
,且它的一条准线与抛物线 的
的
准线重合,则此双曲线的方程为
A.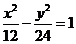 B.
B.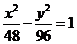 C.
C.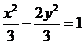 D.
D.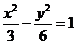

8.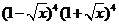 的展开式中
的展开式中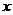 的系数是
的系数是
A.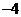 B.
B.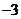 C.3 D.4
C.3 D.4
9.从4名男生和3名女生中选出3人,分别从事三项不同的工作,若这3人中有且只有1
名女生,则选派方案共有
A.108种 B.186种 C.216种 D.270种
10.已知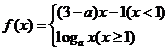 是
是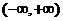 上的增函数,那么
上的增函数,那么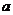 的取值范围是
的取值范围是
A.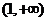 B.
B.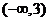 C.
C.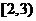 D.(1,3)
D.(1,3)
11.设奇函数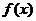 在
在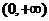 上为增函数,且
上为增函数,且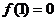 ,则不等式
,则不等式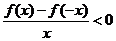 解集
解集
为
A.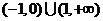 B.
B.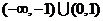

C.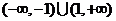 D.
D.

12.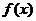 是定义在
是定义在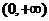 上的非负可导函数,且满足
上的非负可导函数,且满足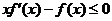 ,对任意正数
,对任意正数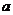 、
、
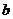 若
若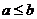 ,则必有
,则必有
A.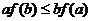 B.
B.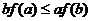

C.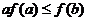 D.
D.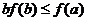


第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题。每小题5分.共20分.把答案填在题中横线上.
13.在某项测量中,测量结果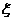 服从正态分布
服从正态分布 ,若
,若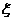 在在(0,1)内取值的 概率为0.4,则
在在(0,1)内取值的 概率为0.4,则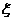 在(0,2)内取值的概率为
.
在(0,2)内取值的概率为
.
14.平面上的向量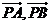 满足
满足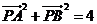 ,且
,且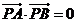 ,若向量
,若向量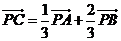 ,
,
则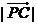 的最大值为
。
的最大值为
。
15.在正方体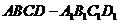 中,
中,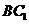 与平面
与平面 所成的角为
.
所成的角为
.
16.给出下列3个命题:
① 命题“存在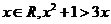 ”的否定是“任意
”的否定是“任意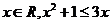 ”;
”;
② “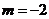 ”是“直线
”是“直线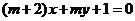 与直线
与直线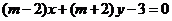 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件;
③ 关于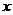 的不等式
的不等式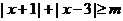 的解集为
的解集为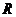 ,则
,则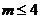 .
.
其中为真命题的序号是
.
三、解答题:本大题共6小题。共70分.解答应写出文宇说明、证明过程或演算步骤.
17.(本小题满分12分)
已知函数 的最小正周期为
的最小正周期为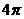 .
.
(1)求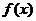 的单调递增区间;
的单调递增区间;
(2)在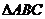 中,角
中,角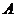 ,
,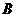 ,
,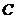 的对边长分别是
的对边长分别是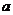 ,
,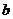 ,
,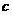 满足
满足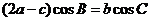 ,求函数
,求函数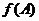 的取值范围.
的取值范围.










18.(本小题满分12分)
有编号为l,2,3,…, 的
的 个学生,入坐编号为1,2,3,…,
个学生,入坐编号为1,2,3,…, 的
的 个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为
个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为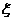 ,已知
,已知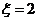 时,共有6种坐法.
时,共有6种坐法.
(1)求 的值;
的值;
(2)求随机变量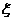 的概率分布列和数学期望.
的概率分布列和数学期望.




19.(本小题满分12分)
已知数列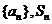 是其前
是其前 项和,且
项和,且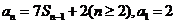 .
.
(1)求数列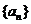 的通项公式;
的通项公式;
(2)设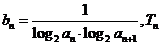 是数列
是数列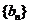 的前
的前 项和,求使得
项和,求使得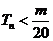 对所有
对所有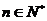 都成立的最小正整数
都成立的最小正整数 。
。






20.(本小题满分12分)
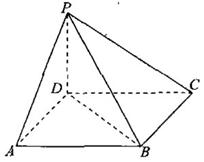 已知四棱锥
已知四棱锥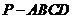 的底面
的底面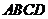 是正方形,且
是正方形,且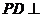 底面
底面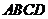 ,其中
,其中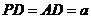 .
.
(1)求二面角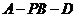 的大小;
的大小;
(2)在线段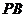 上是否存在一点
上是否存在一点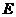 ,使
,使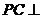 平面
平面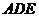 .若存在,试确定
.若存在,试确定 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.



21.(本小题满分10分)
已知椭圆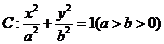 ,过焦点垂直于长轴的弦长为l,且焦点与短轴两端点构成等边三角形.
,过焦点垂直于长轴的弦长为l,且焦点与短轴两端点构成等边三角形.
(1)求椭圆的方程;
(2)过点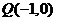 的直线
的直线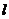 交椭圆于
交椭圆于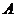 ,
,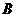 两点,交直线
两点,交直线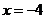 于点
于点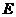 ,点
,点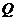 分
分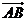 所成比为
所成比为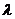 ,点
,点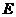 分
分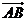 所成比为
所成比为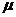 ,求证
,求证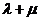 为定值,并计算出该定值.
为定值,并计算出该定值.




22.(本小题满分12分)
已知函数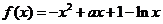 .
.
(1)若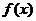 在
在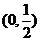 上是减函数,求
上是减函数,求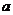 的取值范围;
的取值范围;
(2)函数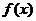 是否既有极大值又有极小值?若存在,求
是否既有极大值又有极小值?若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
一、
1.C 2.D 3.B 4.D 5.D 6.B 7.D 8.A 9.A 10.C
11.D 12.A
1~11.略
12.解: ,
,
 在
在 是减函数,由
是减函数,由 ,得
,得 ,
, ,故选A.
,故选A.
二、
13.0.8 14. 15.
15. 16.①③
16.①③
三、
17.解:(1)

 的单调递增区间为
的单调递增区间为
(2)




18.解:(1)当 时,有
时,有 种坐法,
种坐法,
 ,即
,即 ,
,
 或
或 舍去.
舍去. 
(2) 的可能取值是0,2,3,4
的可能取值是0,2,3,4
又

 的概率分布列为
的概率分布列为

0
2
3
4





则 .
.
19.解:(1) 时,
时, ,
,

又
 ,
,

 是一个以2为首项,8为公比的等比数列
是一个以2为首项,8为公比的等比数列

(2)

 最小正整数
最小正整数 .
.
20.解法一:
(1)设 交
交 于点
于点
 平面
平面 .
.
作 于点
于点 ,连接
,连接 ,则由三垂线定理知:
,则由三垂线定理知: 是二面角
是二面角 的平面角.
的平面角.
由已知得 ,
,
 ,
,
∴二面角 的大小的60°.
的大小的60°.
(2)当 是
是 中点时,有
中点时,有 平面
平面 .
.
证明:取 的中点
的中点 ,连接
,连接 、
、 ,则
,则 ,
,
 ,故平面
,故平面 即平面
即平面 .
.
 又
又 平面
平面 ,
,
 平面
平面 .
.
解法二:由已知条件,以 为原点,以
为原点,以 、
、 、
、 为
为 轴、
轴、 轴、
轴、 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则


(1) ,
,
 ,设平面
,设平面 的一个法向量为
的一个法向量为 ,
,
则 取
取
设平面 的一个法向量为
的一个法向量为 ,则
,则 取
取 .
.
 二面角
二面角 的大小为60°.
的大小为60°.
(2)令 ,则
,则 ,
,
 ,
,
由已知, ,要使
,要使 平面
平面 ,只需
,只需 ,即
,即
则有 ,得
,得 当
当 是
是 中点时,有
中点时,有 平面
平面 .
.
21.解:(1)由条件得 ,所以椭圆方程是
,所以椭圆方程是 .
.

(2)易知直线 斜率存在,令
斜率存在,令
由


由 ,
,
即 得
得
 ,
,
即
得

将 代入
代入
有
22.解:(1)
 在
在 上为减函数,
上为减函数, 时,
时, 恒成立,
恒成立,
即 恒成立,设
恒成立,设 ,则
,则
 时,
时, 在(0,
在(0, )上递减速,
)上递减速,

 .
.
(2)若 即有极大值又有极小值,则首先必需
即有极大值又有极小值,则首先必需 有两个不同正要
有两个不同正要 ,
, ,
,
即 有两个不同正根
有两个不同正根
令
∴当 时,
时, 有两个不同正根
有两个不同正根
不妨设 ,由
,由 知,
知,
 时,
时, 时,
时, 时,
时,
∴当 时,
时, 既有极大值
既有极大值 又有极小值
又有极小值 .www.ks5u.com
.www.ks5u.com