网址:http://m.1010jiajiao.com/timu_id_258918[举报]
一、
1.C 2.D 3.B 4.D 5.D 6.B 7.D 8.A 9.A 10.C
11.D 12.A
1~11.略
12.解: ,
,
 在
在 是减函数,由
是减函数,由 ,得
,得 ,
, ,故选A.
,故选A.
二、
13.0.8 14. 15.
15. 16.①③
16.①③
三、
17.解:(1)

 的单调递增区间为
的单调递增区间为
(2)




18.解:(1)当 时,有
时,有 种坐法,
种坐法,
 ,即
,即 ,
,
 或
或 舍去.
舍去. 
(2) 的可能取值是0,2,3,4
的可能取值是0,2,3,4
又

 的概率分布列为
的概率分布列为

0
2
3
4





则 .
.
19.解:(1) 时,
时, ,
,

又
 ,
,

 是一个以2为首项,8为公比的等比数列
是一个以2为首项,8为公比的等比数列

(2)

 最小正整数
最小正整数 .
.
20.解法一:
(1)设 交
交 于点
于点
 平面
平面 .
.
作 于点
于点 ,连接
,连接 ,则由三垂线定理知:
,则由三垂线定理知: 是二面角
是二面角 的平面角.
的平面角.
由已知得 ,
,
 ,
,
∴二面角 的大小的60°.
的大小的60°.
(2)当 是
是 中点时,有
中点时,有 平面
平面 .
.
证明:取 的中点
的中点 ,连接
,连接 、
、 ,则
,则 ,
,
 ,故平面
,故平面 即平面
即平面 .
.
 又
又 平面
平面 ,
,
 平面
平面 .
.
解法二:由已知条件,以 为原点,以
为原点,以 、
、 、
、 为
为 轴、
轴、 轴、
轴、 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则


(1) ,
,
 ,设平面
,设平面 的一个法向量为
的一个法向量为 ,
,
则 取
取
设平面 的一个法向量为
的一个法向量为 ,则
,则 取
取 .
.
 二面角
二面角 的大小为60°.
的大小为60°.
(2)令 ,则
,则 ,
,
 ,
,
由已知, ,要使
,要使 平面
平面 ,只需
,只需 ,即
,即
则有 ,得
,得 当
当 是
是 中点时,有
中点时,有 平面
平面 .
.
21.解:(1)由条件得 ,所以椭圆方程是
,所以椭圆方程是 .
.

(2)易知直线 斜率存在,令
斜率存在,令
由


由 ,
,
即 得
得
 ,
,
即
得

将 代入
代入
有
22.解:(1)
 在
在 上为减函数,
上为减函数, 时,
时, 恒成立,
恒成立,
即 恒成立,设
恒成立,设 ,则
,则
 时,
时, 在(0,
在(0, )上递减速,
)上递减速,

 .
.
(2)若 即有极大值又有极小值,则首先必需
即有极大值又有极小值,则首先必需 有两个不同正要
有两个不同正要 ,
, ,
,
即 有两个不同正根
有两个不同正根
令
∴当 时,
时, 有两个不同正根
有两个不同正根
不妨设 ,由
,由 知,
知,
 时,
时, 时,
时, 时,
时,
∴当 时,
时, 既有极大值
既有极大值 又有极小值
又有极小值 .www.ks5u.com
.www.ks5u.com
(1)求证数列{bn}是等比数列;
(2)求数列{nbn}的前n项和Tn.
(1)若数列的前n项和为Sn,且a1=b1=d=2,S3<a1004+5b2-2012,求整数q的值;
(2)在(1)的条件下,试问数列中是否存在一项bk,使得bk恰好可以表示为该数列中连续p(p∈N,p≥2)项的和?请说明理由;
(3)若b1=ar,b2=as≠ar,b3=at(其中t>s>r,且(s-r)是(t-r)的约数),求证:数列中每一项都是数列中的项.
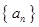 是各项均不为0的等差数列,公差为
是各项均不为0的等差数列,公差为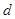 ,
,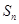 为其前n项和,且满足
为其前n项和,且满足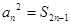 ,
,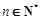 .数列
.数列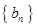 满足
满足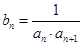 ,
,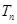 为数列
为数列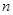 项和.
项和.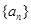 的通项公式
的通项公式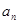 ;
;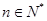 ,不等式
,不等式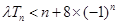 恒成立,求实数
恒成立,求实数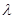 的取值范围;
的取值范围;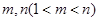 ,使得
,使得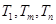 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有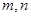
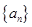 是等比数列,
是等比数列,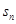 是其前
是其前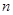 项和.若
项和.若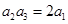 ,且
,且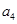 与
与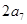 的等差中项为
的等差中项为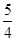 ,则
,则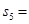 .
.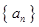 是各项均不为0的等差数列,公差为d,
是各项均不为0的等差数列,公差为d,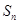 为其前n项和,且满足
为其前n项和,且满足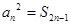 ,
,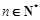 .数列
.数列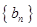 满足
满足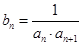 ,
,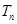 为数列
为数列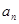 和数列
和数列 ,不等式
,不等式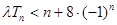 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
 ,使得
,使得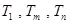 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有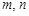 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.