安徽省合肥市2009年高三教学第三次质量检测
数学试题(理)
(考试时间:120分钟 满分:150分)
参考公式:
① 
②球的体积公式:
第Ⅰ卷(满分60分)
一、选择题(本大题共有12个小题,每小题5分,共60分;在每小题给出的四个选项中,只有一项是符合题目要求的)
1、 复数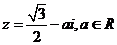 且
且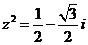 ,则
,则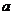 的值为
的值为
A、1
B、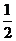 D、
D、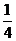
2、已知数列2008,2009, 1,―2008,―2009,…,这个数列的特点是从第二项起,每一项都等于它的前后两项之和,则这个数列的前2009项之和S2009等于
A、2009
B、
3、在三棱锥A―BCD中,侧棱AB、AC、AD两两垂直,△ABC、△ACD、△ADB的面积分别为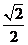 、
、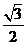 、
、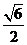 。则三棱锥A―BCD的外接球的体积为
。则三棱锥A―BCD的外接球的体积为
A、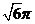 B、
B、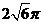 C、
C、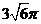 D、
D、 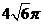
4、不等式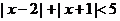 的解集为
的解集为
A、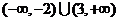 B、
B、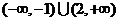 C、
C、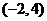 D、
D、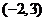
5、已知函数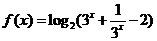 ,则
,则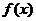 的值域为
的值域为
A、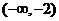 B、
B、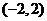 C、
C、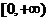 D、
D、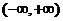
6、从6名男生和2名女生中选出3名志愿者,其中至少有1名女生的选择共有
A、30种 B、36种 C、42种 D、60种
7、对任意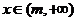 ,不等式
,不等式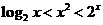 都成立,则m的最小值为
都成立,则m的最小值为
A、2
B、
8、在极坐标系中,直线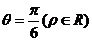 截圆
截圆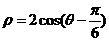 所得弦长是
所得弦长是
A、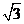 B、
B、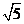 D、 3
D、 3
9、函数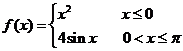 则集合
则集合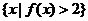 =
=
A、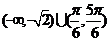 B、
B、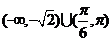 C、
C、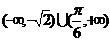 D、
D、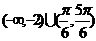
10、设点P(x,y)满足不等式组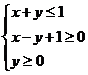 ,则
,则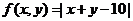 的最大值和最小值分别为
的最大值和最小值分别为
A、11,9 B、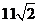 ,
,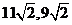 D、
D、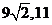
11、对任意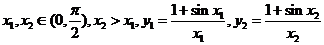 ,则
,则
 A、
A、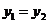 B、
B、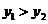 C、
C、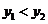 D、
D、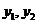 的大小关系不能确定
的大小关系不能确定
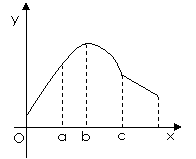
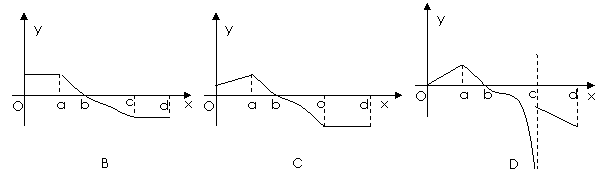
12、已知函数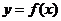 的图像如右图所示,
的图像如右图所示,
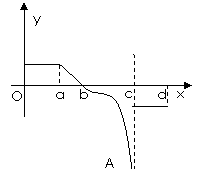 则
则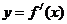 的大致图像可以是
的大致图像可以是
第Ⅱ卷(满分90分)
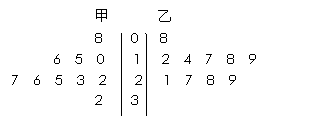
如图是CBA篮球赛中,甲乙两名运动员某赛季一些场次得分的茎叶图,则平均得分高的运动员是________________.
二、填空题(本大题共4小题,每小题4分,共46分)
 14、在2009年春节期间,某市物价部
14、在2009年春节期间,某市物价部
门,对本市五个商场销售的某商品的一
天销售量及其价格进行调查,五个商场
的售价x元和销售量y件之间的一组数
据如下表所示:
价格
9
9.5
10
10.5
11
销售量
11
10
8
6
5
通过分析,发现销售量y对商品价格x具有线性相关关系,则销售量y对商品的价格x的回归直线方程为___________________
15、由两曲线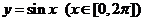 和
和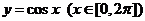 所围成的封闭图形的面积为_______________________
所围成的封闭图形的面积为_______________________
16、在区间(0,2)内任取两数m,n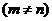 ,则椭圆
,则椭圆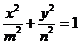 的离心率大于
的离心率大于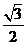 的概率为_____________________
的概率为_____________________
三、解答题(本大题共6小题,共74分;解答应写出文字说明、证明过程或演算步骤)
17、(本小题满分12分)已知函数
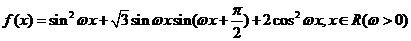 ,在y轴右侧的第一个最高点的横坐标为
,在y轴右侧的第一个最高点的横坐标为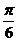 。
。
(1)
求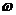 ;
;
(2)
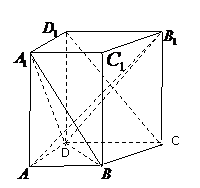 若将函数
若将函数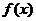 的图像向右平移
的图像向右平移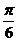 个单位后,再将得到的图像上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图像上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数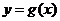 的图像,求函数
的图像,求函数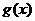 的最大值及单调递减区间。
的最大值及单调递减区间。
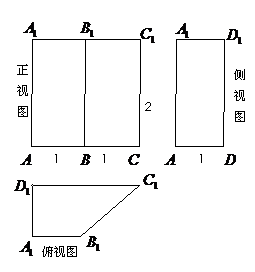 18、(本小题满分12分)四棱柱ABCD―A1B
18、(本小题满分12分)四棱柱ABCD―A1B
(1)求证: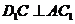 ;
;
(2)设E是DC上一点,
试确定E的位置,使
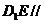 平面A1BD,并说
平面A1BD,并说
明理由;
(3) 在(2)的结论
成立时,求直线BE和
平面A1BD所成角的正弦值。
 19、(本小题满分12分)请看右边的程序框图:若
19、(本小题满分12分)请看右边的程序框图:若
依次输入m=0,1,2,3,4,……,(m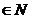 )则
)则
由右边程序框图输出的数值A组成一个数列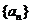
(1)
求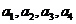 和数列
和数列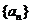 的通项公式;
的通项公式;
(2)
若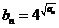 ,求数列{
,求数列{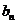 }的前n项和Sn
}的前n项和Sn
20、(本小题满分12分)有一高二学生盼望进入某名牌
大学由以下每种方式都可录取:
① 2010年2月国家数学奥赛集训队考试通过(集训队
从2009年10月省数学竞赛一等奖中选拔):
② 2010年3月自主招生考试通过并且2010年6月高考
分数达重点线;
③ 2010年6月高考达到该校录取分数线(该校录取分数线
高于重点线)。
该考生具有参加省数学竞赛、自主招生和高考的资格且估计
自己通过各种考试的概率如下表:
省数学竞赛一等奖
自主招生通过
高考达重点线
高考达该校分数线
0.5
0.7
0.8
0.6
如果数学竞赛获一等奖,该学生估计自己进入国家集训队的概率是0.4。若进入国家集训队,则提前录,若未被录取,则再按② ③的顺序依次录取;前面已被录取后,不得参加后面的考试或录取。
(1) 求该考生参加自主招生考试的概率;
(2)
求该学生参加考试的次数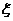 的分布列及数学期望;
的分布列及数学期望;
(3) 求该学生被该校录取的概率。
21、(本小题满分12分)设向量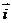 ,
,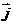 为直角坐标平面内x轴、y轴正方向上的单位向量,若向量
为直角坐标平面内x轴、y轴正方向上的单位向量,若向量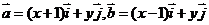 ,且
,且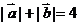 。
。
(1)求满足上述条件的点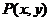 的轨迹C的方程;
的轨迹C的方程;
(2)过F(―1,0)任作一条与y轴不垂直的直线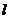 交轨迹于A、B两点,在x轴上是否存在点M,使得MF平分∠AMB,若存在,求出点M的坐标;若不存在,请说明理由。
交轨迹于A、B两点,在x轴上是否存在点M,使得MF平分∠AMB,若存在,求出点M的坐标;若不存在,请说明理由。
22、(本小题满分14分)已知函数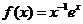 的定义域为(0,
的定义域为(0,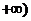 。
。
(1)求函数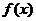 在[m,m+1] (m>0)上的最小值;
在[m,m+1] (m>0)上的最小值;
(2)对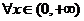 ,不等式
,不等式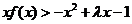 恒成立,求
恒成立,求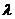 的取值范围。
的取值范围。





