喀什第二中学2008-2009学年高一年级第二学期第二次月考
数学试题
(人教版必修四第二章平面向量、必修五第二章数列、必修二第一章空间几何体)
2009.4.25
本试卷分第Ⅰ卷(基础知识,满分100分)、第Ⅱ卷(按较高要求命题,满分50分)、答题纸三部分,第Ⅰ卷第1页至第3页,第Ⅱ卷第3页,答题纸第4页至第7页。全卷满分150分,考试时间120分钟。
注意事项:
1、 答题前,务必在试题卷、答题卷规定的地方填写自己的班级、姓名、考号。
2、 所有答题务必用钢笔或圆珠笔写在答题纸上指定位置,用铅笔答题无效。
3、 考试结束,监考教师仅收回答题卷,试题卷由学生带回并保管好。
参考公式:球体的体积公式 v= 表面积 S表=S底+S侧
表面积 S表=S底+S侧
柱体的体积 V=sh 锥体的体积 V= 长方体的体积 V=长×宽×高
长方体的体积 V=长×宽×高
第 Ⅰ 卷 (按基础知识要求命题,满分100分)
Ⅰ 卷 (按基础知识要求命题,满分100分)
一、选择题:(每题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求,将正确答案的字母填入答题卷中,题目中的黑体字字母代表向量)
1、下列等式不成立的是 ( )
A、 a+0=a B、a+b=b+a C、 +
+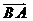
 = 2
= 2 D、
D、 +
+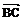 =
=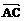
2、A(3,1) B(2,-1)则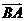 的坐标是( )
的坐标是( )
A、 (-2,-1) B、 (2,1) C、 (1,2) D、 (-1,-2)
3、若a =(2,1),b =(1,0)则
A、 (5,3) B、 (4,3) C、 (8,3) D、 (0,-1)
4、a =(-1,2),b =(2,y)若a ∥b 则 y的值是( )
A、 1 B、
5、若 | m|=4,| n|=6,m 与n的夹角为450 ,则m?n = ( )
A、 12 B、 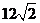 C、 -
C、 -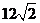 D、 -12
D、 -12
6、在数列{an}中,an+2= an+1+ an,且a1=2,a2=5,则a5=( )
A、-3
B、
7、在等比数列{an}中,已知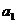 =3,q=2则a5=( )
=3,q=2则a5=( )
A、48
B、
8、等比数列{an}中的各项都是正数,若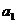 =81,a5=16,则它的前3项和是( )
=81,a5=16,则它的前3项和是( )
A、179
B、
9、等比数列{an}中的各项都是正数.若a1=16,a3=9,则a2=( )

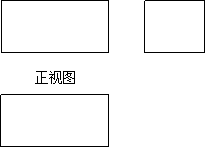 A、12 B、
A、12 B、
10、右图所示的是一个立体图形的三视图,请说出该立体图形的名称为( )
A、圆柱 B、棱锥
 C、长方体 D、棱台
C、长方体 D、棱台
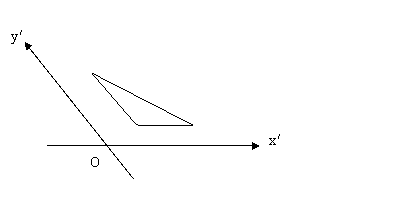
11、如图,直观图表示的平面图形是( )
A、任意三角形 B、锐角三角形
C、直角三角形 D、钝角三角形
12、水平放置的正方形的直观图是( )
A、平行四边形 B、三角形
C、梯形 D、圆
二、填空题:(每题4分,共16分,将正确答案填入答题卷中)
13、已知A(-3,2),B(0,-2)则| 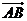 |=
|=
14、棱长为1,各面都是正三角形的四面体的表面积为
15、已知数列{an}的前n项和为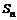 ,且
,且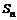 =
=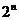 - 1,则an=
- 1,则an=
16、等比数列的首项是1,末项是8,公比是2,则这个数列的项数是
三、解答题:(共36分,解答应写出文字说明、证明过程或演算步骤,请在答题卷中作答)
17、(本题12分)已知a =(4,3),b =(-1,2)
(1)、求a 与b 的夹角θ的余弦值
(2)、若向量a ?λb与
18、(本题6分)下图为一个几何体的三视图
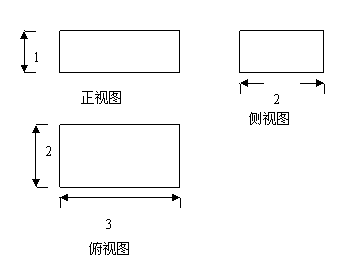 求该几何体的表面积和体积
求该几何体的表面积和体积
19、(本题6分)若数列{an}是等差数列, a4=38, a8=78,求an及Sn
20、(本题12分)已知数列{an}的前n项和Sn=2n2 + n,求数列的通项an
第 Ⅱ 卷 (按较高要求命题,满分50分)
Ⅱ 卷 (按较高要求命题,满分50分)
一、选择题:(本大题共2小题,每小题4分,共8分.在每小题给出的四个选项中,只有一项是符合题目要求的)
21、已知a、b、c、d成等比数列且曲线y=x2-2x+3的顶点是(b,c),则a×d=( )
A、3
B、
22、三个球的半径之比为1:2:3,那么最大的球的体积是其它两个球的体积之和的( )
A 1倍 B、2倍 C、3倍 D、4倍
二、填空题:(本大题共3小题,每小题4分,共12分。在答题卡上的相应题目的答题区域内作答)
 23、水平放置的三角形ABC的斜二测直观图如图所示,已知A'C'=3 B'C'=2,则AB边上的中线的实际长度为
23、水平放置的三角形ABC的斜二测直观图如图所示,已知A'C'=3 B'C'=2,则AB边上的中线的实际长度为
24、若棱长为1的正方体的顶点都在同一个球面上,则该球的表面积为
25、已知数列{an}中的通项公式是an=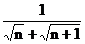 若其前n项和为10,
若其前n项和为10,
则项数n为
三、解答题:(本大题共3小题,共30分。解答应写出文字说明、证明过程或演算步骤,请在答题卷中作答)
26、(本题6分)已知点A(3,-4),B(-1,2),点p在直线AB上,且 ,求点p的坐标。
,求点p的坐标。
27、(本题14分)已知等差数列{an}中,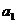 =20且S10=S15,,那么n为何值时,Sn有最大值,并求出它的最大值。
=20且S10=S15,,那么n为何值时,Sn有最大值,并求出它的最大值。
28、(本题10分)数列{an}的前n项和为Sn,Sn=2an--1(n∈N*)
求{an}的通项公式。
喀什第二中学2008--2009学年高一年级第二学期第二次月考
答题纸
(人教版必修四第二章平面向量、必修五第二章数列、必修二第一章空间几何体)
第 Ⅰ 卷 (按基础知识要求命题,满分100分)
Ⅰ 卷 (按基础知识要求命题,满分100分)
 二、填空题:(每题4分,共16分,将正确答案填入下面横线上)
二、填空题:(每题4分,共16分,将正确答案填入下面横线上)
13._____; 14.______; 15._______; 16. ______.
三、解答题:(共36分)解答应写出文字说明、证明过程或演算步骤,请在答题卷中作答。
17.(本题12分)
(1)(满分6分)
(2)(满分6分)
18.(本题6分)
19.(本题6分)
题号
分数
Ⅰ卷选择
Ⅰ卷填空
17
18
19
20
合计
Ⅱ卷选择
Ⅱ卷填空
26
27
28
合计
20.(本题12分)
第 Ⅱ 卷 (按较高要求命题,满分50分)
Ⅱ 卷 (按较高要求命题,满分50分)
一、选择题:(本大题共2小题,每小题4分,共8分.在每小题给出的四个选项中,只有一项是符合题目要求的,将正确答案填入下面横线上)
21.________;22.__________
二、填空题:(本大题共3小题,每小题4分,共12分。将正确答案填入下面横线上)
23._________;24.________;25._______ .
三、解答题:(本大题共3小题,共30分.解答应写出文字说明、证明过程或演算步骤,请在答题卷中作答)
26.(本题6分)
27.(本题14分)
28、(本题10分)
喀什第二中学2008--2009学年高一年级第二学期第二次月考
评分细则
第 Ⅰ 卷 (按基础知识要求命题,满分100分)
Ⅰ 卷 (按基础知识要求命题,满分100分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
C
D
B
D
A
B
A
C
C
A
二、填空题:(每题4分,共16分,将正确答案填入下面横线上)
13. 5 ; 14.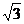 ; 15.
; 15.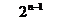 ; 16.
; 16.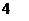 .
.
三、解答题:(共36分)解答应写出文字说明、证明过程或演算步骤,请在答题卷中作答。
17.(本题12分)
(1)(满分6分)
∵a =(4,3),b =(-1,2)
∴a?b =4×(-1)+3×2=-4+6=2 ----------------------------------------2分
| a |=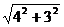 =5
------------------------------------------3分
=5
------------------------------------------3分
| b |=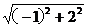 =
=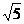 ------------------------------------------4分
------------------------------------------4分
∴cosθ=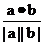 =
=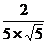 =
= ------------------------------------------6分
------------------------------------------6分
(2)(满分6分)
∵向量a ?λb与
∴(a ?λb)?(
即
∴2×52+2(1-2λ)-5λ=0 ---------------------------------------------------------------------11分
∴λ=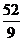 ----------------------------------------------------------------------12分
----------------------------------------------------------------------12分
18.(本题6分)
解:该几何体为长方体,其直观图为

∴该几何体的表面积为S=(1×2+1×3+2×3)×2=22 -------------------------------3分
体积为V=1×2×3=6 ------------------------------------------------------------------------6分
19.(本题6分)
解:设等差数列{an}的首项是a1,公差为d
由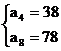 得到
得到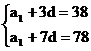 -----------------------------2分
-----------------------------2分
解得 ----------------------------3分
----------------------------3分
∴an=a1+(n-1)d
=8+(n-1)×10
=10n-2 -----------------------------4分
Sn=na1+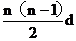
=8n+5n2-5n=5n2+3n ------------------------------6分
20.(本题12分)
解:当n≥2时
an= Sn- Sn-1 ------------------------------------------------------------5分
=2n2+n-[2(n-1)2+n-1]
=2n2+n-[2n2-3n+1]
=4n-1 ----------------------------------------10分
当n=1时
a1=S1=3适合上式
∴an=4n-1 -----------------------------------------------------------12分
第 Ⅱ 卷 (按较高要求命题,满分50分)
Ⅱ 卷 (按较高要求命题,满分50分)
题号
21
22
答案
B
C
二、填空题:(本大题共3小题,每小题4分,共12分。在答题卡上的相应题目的答题区域内作答)
23.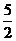 ; 24.3π;
25.120
; 24.3π;
25.120
三、解答题:(本大题共3小题,共30分。解答应写出文字说明、证明过程或演算步骤,请在答题卷中作答)
26、(本题6分)
∵点p在直线AB上且
∴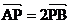 或
或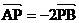 ,-------------------------------------------2分
,-------------------------------------------2分
设p点坐标为(x,y)
当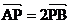 时
时
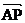 =(x-3,y+4)
=(x-3,y+4) 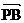 =(-1-x,2-y)
=(-1-x,2-y)
∴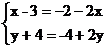
∴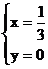 -----------------------------------------------4分
-----------------------------------------------4分
当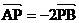
有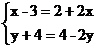
∴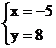 -----------------------------------------------5分
-----------------------------------------------5分
∴点p的坐标为(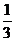 ,0)或(-5,8)
-----------------------------------6分
,0)或(-5,8)
-----------------------------------6分
27.(本题14分)
解:设等差数列公差为d---------------------------------------------1分
由a1=20 S10=S15,得到
10×20+ =15×20+
=15×20+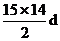 ----------------------------------3分
----------------------------------3分
∴45d+200=300+105d
∴d=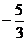 --------------------------------------5分
--------------------------------------5分
∴Sn=20n+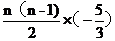 ----------------------------------------7分
----------------------------------------7分
=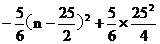 -------------------------------------9分
-------------------------------------9分
∴当n=12或者13时,Sn有最大值--------------------------------12分
并且最大值为
S12=S13=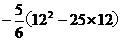 =130 -------------------------------14分
=130 -------------------------------14分
法二:
设公差为d,由a1=20 S10=S15,得到
10×20+ =15×20+
=15×20+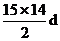 ----------------------------------3分
----------------------------------3分
∴45d+200=300+105d
∴d=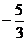 ---------------------------------------------5分
---------------------------------------------5分
∵S10=S15,
∴S15-S10=a11+a12+a13+a14+a15=0 ---------------------------------------------7分
∵a11+a15=a12+a14=
∴a13=0 -----------------------------------------------------8分
∵d<0,a1>0
∴a1,a2,a3,…,a12均为正数
而a14以后各项都是负数 ----------------------------------------------9分
∴当n=12或者13时,Sn有最大值 -------------------------10分
S12=S13=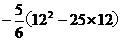 =130
------------------------------12分
=130
------------------------------12分
28.(本题10分)
解:当n=1时,S1=
∴a1=1 -------------------------------------------------------------------------------2分
当n≥2时an=Sn-Sn-1=2an-1-2an-1 +1-----------------------------6分
∴an=2an-1--------------------------------------------------------8分
∴{an}是以1为首项,以2为公比的等比数列 ----------------------9分
∴an=1×2n-1=2n-1 ---------------------------------------------10分