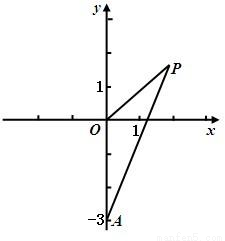
摘要:∴或.-------------------------------------------2分设p点坐标为(x.y)
网址:http://m.1010jiajiao.com/timu_id_157589[举报]
 (选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
(选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.A.选修4-1:几何证明选讲
如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过
N点的切线交CA的延长线于P.
(1)求证:PM2=PA•PC;
(2)若⊙O的半径为2
| 3 |
| 3 |
B.选修4-2:矩阵与变换
曲线x2+4xy+2y2=1在二阶矩阵M=
|
C.选修4-4:坐标系与参数方程
在极坐标系中,圆C的极坐标方程为ρ=
| 2 |
| π |
| 4 |
|
D.选修4-5:不等式选讲
设a,b,c均为正实数.
(1)若a+b+c=1,求a2+b2+c2的最小值;
(2)求证:
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
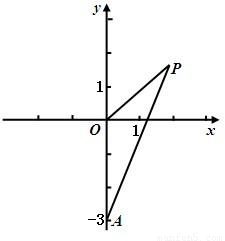
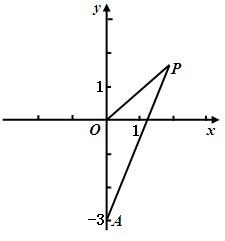 如图,已知点A(0,-3),动点P满足|PA|=2|PO|,其中O为坐标原点.
如图,已知点A(0,-3),动点P满足|PA|=2|PO|,其中O为坐标原点.(Ⅰ)求动点P的轨迹方程.
(Ⅱ)记(Ⅰ)中所得的曲线为C.过原点O作两条直线l1:y=k1x,l2:y=k2x分别交曲线C于点E(x1,y1)、F(x2,y2)、G(x3,y3)、H(x4,y4)(其中y2>0,y4>0).求证:
| k1x1x2 |
| x1+x2 |
| k2x3x4 |
| x3+x4 |
(III)对于(Ⅱ)中的E、F、G、H,设EH交x轴于点Q,GF交x轴于点R.求证:|OQ|=|OR|.(证明过程不考虑EH或GF垂直于x轴的情形) 查看习题详情和答案>>
如图,已知点A(0,-3),动点P满足|PA|=2|PO|,其中O为坐标原点,动点P的轨迹为曲线C,过原点O作两条直线分别l1:y=k1x,l2:y=k2x交曲线C 于点E(x1,y1)、F(x2,y2)、G(x3,y3)、H(x4,
y4)(其中y2>0,y4>0)。
y4)(其中y2>0,y4>0)。
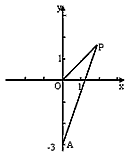
(1)求证: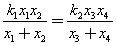 ;
;
(2)对于(1)中的E、F、G、H,设EH交x轴于点Q,GF交x轴于点R。求证:|OQ|=|OR|。(证明过程不考虑EH或GF垂直于x轴的情形)
查看习题详情和答案>>
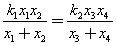 ;
;(2)对于(1)中的E、F、G、H,设EH交x轴于点Q,GF交x轴于点R。求证:|OQ|=|OR|。(证明过程不考虑EH或GF垂直于x轴的情形)
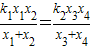 ;
;
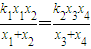 ;
;