贵州省2009届高三高招适应性考试
数学(文史类)
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两不分。第I卷1至2页。第Ⅱ卷3至4页。
第I卷
(本卷共12小题,每小题5分,共60分)
注意事项:
1.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,不能答在试题卷上。
2.答题前请认真阅读答题卡上的“注意事项”。
参考公式:
如果事件 、
、 互斥,那么
球的表面积公式
互斥,那么
球的表面积公式


如果事件 、
、 相互独立,那么
其中
相互独立,那么
其中 表示球的半径
表示球的半径
 球的体积公式
球的体积公式
如果事件 在一次实验中发生的概率是
在一次实验中发生的概率是 ,那么
,那么 
 次独立重复实验中事件
次独立重复实验中事件 恰好发生
恰好发生 次的概率 其中
次的概率 其中 表示球的半径
表示球的半径

在每小题给出的四个选项中,只有一项是符合题目要求的。
一、选择题
1.设集合 、
、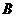 是全集
是全集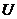 的两个子集,则“
的两个子集,则“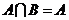 ”是“
”是“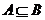 ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.已知点 在第三象限,且
在第三象限,且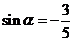 ,则
,则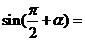
A.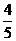 B.
B.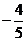 C.
C.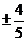 D.
D.
3.已知数列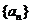 的通项
的通项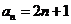 ,前
,前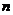 项和为
项和为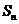 ,若数列
,若数列 的前
的前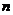 项和
项和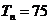 ,则
,则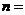
A.8
B.
4.过点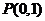 与圆
与圆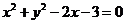 相交的所有直线中,被圆截得的弦最短时的直线方程是
相交的所有直线中,被圆截得的弦最短时的直线方程是
A.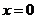 B.
B.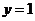 C.
C.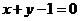 D.
D.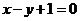
5.已知定义在 上的函数
上的函数 为奇函数,且当
为奇函数,且当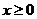 时
时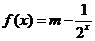 ,则
,则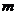 的值为
的值为
A.0
B.
6.在5张卡片上分别写着1、2、3、4、5,混合后再任意排成一行,则得到的五位数能被2或5整除的概率为
A.0.2
B.
7.若定义在 上的偶函数
上的偶函数 的最小正周期是
的最小正周期是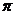 ,且当
,且当 时,
时,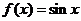 ,则
,则 的值为
的值为
A.1
B. C.
C. D.
D.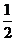
8.在四棱锥 中,底面是边长为1的菱形,
中,底面是边长为1的菱形, 底面
底面 ,则异面直线
,则异面直线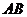 与
与 所成角的余弦值为
所成角的余弦值为
A. B.
B. C.
C.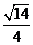 D.
D.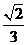
9.已知 、
、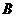 两点的坐标分别为
两点的坐标分别为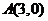 、
、 ,
,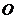 是原点,点
是原点,点 在线段
在线段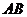 上,若
上,若
 ,则
,则 的取值范围是
的取值范围是
A.(1,9) B.(0,9) C.[0,9] D.[1,9]
10.已知双曲线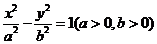 的右焦点为
的右焦点为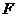 ,若过点
,若过点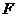 且倾斜角为60°的直线与双曲线渐近线平行,则此双曲线离心率的值为
且倾斜角为60°的直线与双曲线渐近线平行,则此双曲线离心率的值为
A.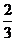 B.
B.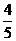 D.3
D.3
11.函数 是偶函数,则曲线
是偶函数,则曲线 在
在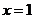 处的切线方程是
处的切线方程是
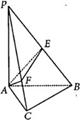 A.
A.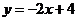 B.
B.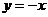 C.
C. D.
D.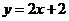
12.如图,在三棱锥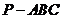 中,
中,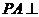 底面
底面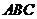 ,
,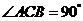 ,
,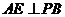
于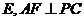 于
于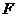 ,若
,若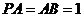 ,则当
,则当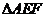 的面积最大时,
的面积最大时,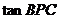
等于
A.2
B.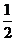 C.
C. D.
D.
第Ⅱ卷
(本卷共10小题,共90分)
注意事项:
1.考生不能将答案直接答在试卷上,必须答在答题卡上。
二、填空题:本大题共4小题,每小题5分,共20分,大答案填在答题卡上。
13.设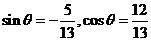 ,则
,则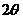 的终边所在象限是第______________象限。
的终边所在象限是第______________象限。
14.在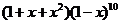 的展开式中,含
的展开式中,含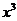 项的系数是_____________。
项的系数是_____________。
15.若实数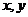 满足
满足 ,则
,则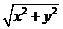 的取值范围是_____________。
的取值范围是_____________。
16.若等比数列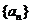 中,
中,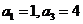 ,则
,则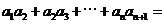 ___________。
___________。
三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分10分)
已知向量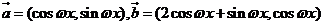 ,其中
,其中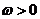 ,
,
记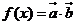 ,若函数
,若函数 的最小正周期是
的最小正周期是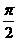 。
。
(I)求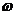 的值;
的值;
(Ⅱ)求 的最小值和使
的最小值和使 取得最小值的
取得最小值的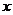 的集合。
的集合。
18.(本小题满分12分)
汉方集团用三辆客车送职工去黄果树旅游,从贵阳到黄果树有清黄高速公路和贵黄高等
级公路两条公路,已知客车走贵黄公路堵车的概率为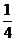 ;若1号、2号两辆客车走贵黄公路。
;若1号、2号两辆客车走贵黄公路。
3号客车走清黄公路,且三辆客车是否堵车相互之间没有影响,若三辆客车中恰有一辆被堵
车的概率为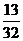
(I)求客车走清黄公路堵车的概率;
(Ⅱ)求三辆客车中至少有一辆被堵车的概率。
19.(本小题满分12分)
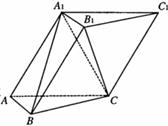
如图,在三棱柱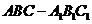 中,所有的棱长都为2,
中,所有的棱长都为2,
侧面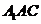 与底面
与底面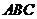 垂直,
垂直,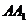 与底面
与底面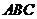 所成角为
所成角为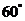 。
。
(I)求证: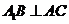 ;
;
(Ⅱ)求平面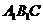 与平面
与平面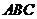 所成的二面角(锐角)的大
所成的二面角(锐角)的大
小
20.(本小题满分12分)
已知等差数列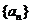 中
中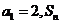 为前
为前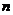 项和,且
项和,且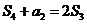 ;等比数列
;等比数列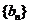 满足
满足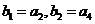 。
。
(I)求数列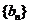 的通项公式;
的通项公式;
(Ⅱ)设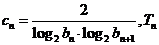 为数列
为数列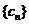 的前
的前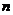 项的和,
项的和,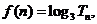 求
求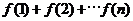 。
。
21.(本小题满分12分)
设函数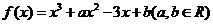 ,若
,若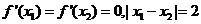 。
。
(I)求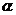 的值及函数
的值及函数 的单调区间;
的单调区间;
(Ⅱ)若存在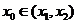 ,使得
,使得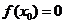 ,求
,求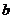 的取值范围。
的取值范围。
22.本小题满分12分
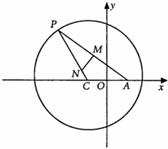 已知圆
已知圆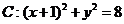 ,定点
,定点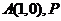 为圆上一
为圆上一
动点,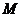 是
是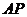 的中点,点
的中点,点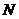 在
在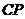 上,若
上,若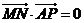 ,
,
(I)求点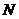 的轨迹
的轨迹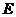 的方程;
的方程;
(Ⅱ)若直线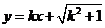 与曲线
与曲线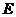 交于不同两点
交于不同两点
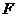 、
、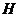 ,
, 是坐标原点,
是坐标原点,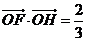 ,求
,求