2009年广西省柳州市初中毕业升学考试
数学试卷
(考试时间共120分钟,全卷满分120分)
第Ⅰ卷(选择题,共18分)
注意事项:
1.答题前,考生务必先将自己的姓名、准考证号用蓝、黑色墨水笔或圆珠笔填写在试卷左边的密封线内.
2.第Ⅰ卷为第1页至第二页.答题时,请用2B铅笔把各小题正确答案序号填涂在答题卡对应的题号内.如需改动,须用橡皮擦干净后,再填涂其它答案.
在第Ι卷上答题无效.
一、选择题(本大题共6小题,每小题3分,满分18分.在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得零分)
1.在3,0,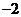 ,
,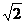 四个数中,最小的数是( )
四个数中,最小的数是( )
A.3 B.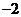 D.
D.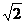
2.如下图所示,图中三角形的个数共有( )
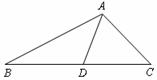
A.1个 B.2个 C.3 个 D.4个
3.若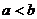 ,则下列各式中一定成立的是( )
,则下列各式中一定成立的是( )
A.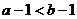 B.
B.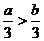 C.
C.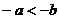 D.
D.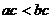
4.某学习小组7个男同学的身高(单位:米)为:1.66、1.65、1.72、1.58、1.64、1.66、1.70,那么这组数据的众数为( )
A.1.65 B.
5.分式方程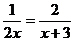 的解是( )
的解是( )
A.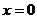 B.
B.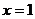 C.
C.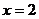 D.
D.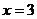
6.一根笔直的小木棒(记为线段AB),它的正投影为线段CD,则下列各式中一定成立的是( )
A.AB=CD B.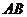 ≤
≤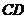 C.
C.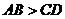 D.
D.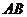 ≥
≥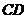
第Ⅱ卷(非选择题,满分102分)
二、填空题(本大题共10小题,每小题3分,满分30分. 请将答案直接填写在题中横线上的空白处)
7.计算: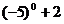 = .
= .
8.请写出一个是轴对称图形的图形名称。答: .
9.计算: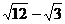 = .
= .
10.在如下图中,直线AB∥CD,直线EF与AB、CD分别相交于点E、F,如果∠1=46°,那么∠2= °.

11.一个物体现在的速度是
12.因式分解: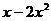 =
.
=
.
13.反比例函数  的图象经过点(2,1),则
的图象经过点(2,1),则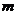 的值是 .
的值是 .
14.在一个不透明的口袋中装有若干个只有颜色不同的球,如果已知袋中只有4个红球,且摸出红球的概率为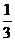 ,那么袋中的球共有 个.
,那么袋中的球共有 个.
15.如下图,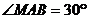 ,
,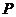 为
为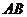 上的点,且
上的点,且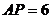 ,圆
,圆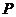 与
与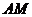 相切,则圆
相切,则圆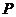 的半径为 .
的半径为 .
16.矩形内有一点P到各边的距离分别为1、3、5、7,则该矩形的最大面积为 平方单位.
三、解答题(本大题10小题,满分72分.解答应写出必要的文字说明、演算步骤或推理过程)
17.(本题满分6分)
先化简,再求值: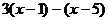 ,其中
,其中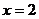 .
.
18.(本题满分6分)
解不等式组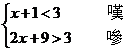 ,并把它的解集表示在数轴上.
,并把它的解集表示在数轴上.
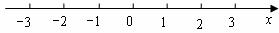
19.(本题满分6分)
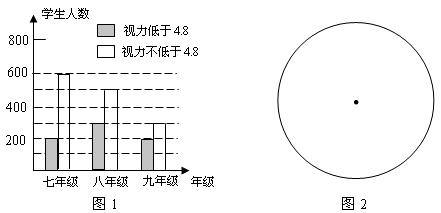
某学习小组对所在城区初中学生的视力情况进行抽样调查,图1是这些同学根据调查结果画出的条形统计图.请根据图中信息解决下列问题:
(1)本次抽查活动中共抽查了多少名学生?
(2)请估算该城区视力不低于4.8的学生所占的比例,用扇形统计图在图2中表示出来.
(3)假设该城区八年级共有4000名学生,请估计这些学生中视力低于4.8的学生约有多少人?
20.(本题满分6分)
如下图,四边形ABCD中,AB∥CD,∠B=∠D,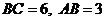 ,求四边形ABCD的周长.
,求四边形ABCD的周长.

21.(本题满分6分)
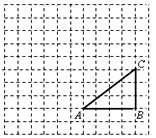
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到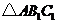 .
.
(1)在正方形网格中,作出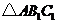 ;(不要求写作法)
;(不要求写作法)
(2)设网格小正方形的边长为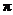 )
)
22.(本题满分6分)
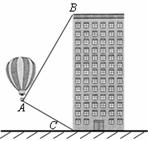
如下图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为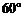 ,看这栋高楼底部的俯角为
,看这栋高楼底部的俯角为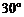 ,热气球与高楼的水平距离为
,热气球与高楼的水平距离为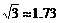 )
)
23.(本题满分8分)
如下图,直线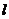 与
与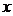 轴、
轴、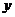 轴分别交于点
轴分别交于点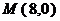 ,点
,点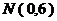 .点
.点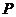 从点
从点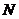 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿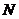 →
→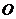 方向运动,点
方向运动,点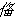 从点
从点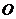 出发,以每秒2个单位长度的速度沿
出发,以每秒2个单位长度的速度沿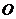 →
→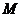 的方向运动.已知点
的方向运动.已知点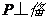 同时出发,当点
同时出发,当点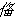 到达点
到达点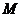 时,
时,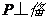 两点同时停止运动,设运动时间为
两点同时停止运动,设运动时间为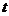 秒.
秒.
(1)设四边形MNPQ的面积为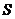 ,求
,求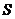 关于
关于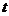 的函数关系式,并写出
的函数关系式,并写出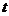 的取值范围.
的取值范围.
(2)当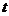 为何值时,
为何值时,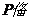 与
与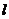 平行?
平行?
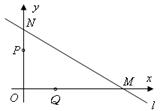
24.(本题满分8分)
某校积极推进“阳光体育”工程,本学期在九年级11个班中开展篮球单循环比赛(每个班与其它班分别进行一场比赛,每班需进行10场比赛).比赛规则规定:每场比赛都要分出胜负,胜一场得3分,负一场得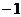 分。
分。
(1)如果某班在所有的比赛中只得14分,那么该班胜负场数分别是多少?
(2)假设比赛结束后,甲班得分是乙班的3倍,甲班获胜的场数不超过5场,且甲班获胜的场数多于乙班,请你求出甲班、乙班各胜了几场.
25.(本题满分10分)
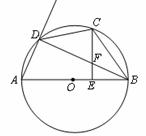
如下图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
(1)求证: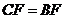 ;
;
(2)若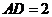 ,⊙O的半径为3,求BC的长.
,⊙O的半径为3,求BC的长.
26.(本题满分10分)
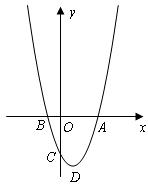
如下图,已知抛物线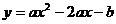 (
(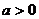 )与
)与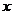 轴的一个交点为
轴的一个交点为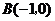 ,与y轴的负半轴交于点C,顶点为D.
,与y轴的负半轴交于点C,顶点为D.
(1)直接写出抛物线的对称轴,及抛物线与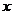 轴的另一个交点A的坐标;
轴的另一个交点A的坐标;
(2)以AD为直径的圆经过点C.
①求抛物线的解析式;
②点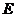 在抛物线的对称轴上,点
在抛物线的对称轴上,点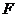 在抛物线上,且以
在抛物线上,且以 四点为顶点的四边形为平行四边形,求点
四点为顶点的四边形为平行四边形,求点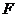 的坐标.
的坐标.