2008-2009年淄博市临淄区第二学期初二期中考试
数学试卷
一、选择题(本题共10小题,在每小题所给出的四个选项中,只有一个是正确的。每小题3分,满分30分,错选、不选或选出的答案超过一个,均记0分.)
1.在平面直角坐标系中,点P(-1,2)的位置在
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
2.已知点A(0,a)到x轴的距离是3,则a为
(A)3 (B)-3 (C)±3 (D)±6
3.如图,小明从点O出发,先向西走
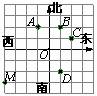
(A)点A (B)点B (C)点C (D)点D
4.如下图,下列各点在阴影区域内的是
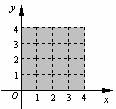
(A)(3,2) (B)(-3,2)
(C)(3,-2) (D)(-3,-2)
5.下列句子中不是命题的是
(A)两直线平行,同位角相等. (B)直线AB垂直于CD吗?
(C)若?a?=?b?,则a 2 = b 2. (D)同角的补角相等
6.能将一个三角形分成面积相等的两个三角形的一条线段是
(A)中线 (B)角平分线 (C)高线 (D)任意一条线段
7.如下图,∠1=75º,要使a∥b,则∠2等于
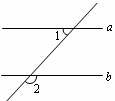
(A)75º (B)95º
(C)105º (D)115º
8.下列长度的三条线段能组成三角形的是
(A)3,4,8 (B)5,6,11 (C)5,5,10 (D)5,6,10
9.若∠A和∠B的两边分别平行,则∠A比∠B的2倍少30°,则∠B的度数为
(A)30° (B)70° (C)30°或70° (D)30°或150°
10.为了美化城市,建设中的某休闲广场准备用某种正多边形地砖与厚度、边长相同的正方形地板砖组合铺砌地面,在正三角形、正六边形、正八边形、正十二边形四种形状的地板砖,可供选择的材料有( )种.
(A)1
(B)
二、填空题(每小题3分,共30分)
11.如图是永州市几个主要景点示意图,根据图中信息可确定九疑山的中心位置C点的坐标为 .

12.将点(1,2)向左平移1个单位,再向下平移2个单位后得到对应点的坐标是 .
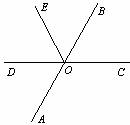
13.如图,直线AB、CD相交于点O,OE平分∠BOD.若∠AOC=120°,则∠BOE= .
14.一个多边形的内角和是外角和的2倍,则它是 边形.
15.直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38o ,则∠COB= .
16.已知△ABC 的∠B 和∠C 的平分线BE,CF交于点G,∠A=100 o ,则∠BGC = .
17.已知等腰三角形的一边等于4,一边等于9,则它的周长是 .
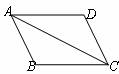
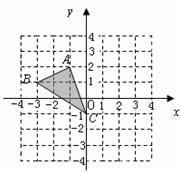
18.如图,□ABCD中,∠ADC=125°,∠CAD=22°,则∠CAB= .
19.将杨辉三角中的每一个数都换成分数,得到一个如下图所示的分数三角形,称莱布尼茨三角形.若用有序实数对(m,n)表示第m行,从左到右第n个数,

如(4,3)表示分数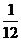 。那么(9,2)表示的分数是 .
。那么(9,2)表示的分数是 .
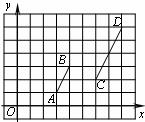
20.线段AB,CD在平面直角坐标系中的位置如下图所示,O为坐标原点.若线段AB
上一点P的坐标为(a,b),则直线OP与线段CD的交点的坐标是 .
三、作图题(第21、22题每小题5分,第23题6分,共16分)
21.画出将 向右平移2个单位得到的
向右平移2个单位得到的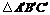 ,并写出A点的对应点A′的坐标.
,并写出A点的对应点A′的坐标.
22.在某城市中,体育场在火车站以西

23.过顶点A分别画出 的中线、角平分线和高.
的中线、角平分线和高.

四、解答题(第24、25、26每题6分,第27、28题每题8分,共34分)
24.已知,如图,∠1=∠ABC=∠ADC,∠3=∠5,∠2=∠4,∠ABC+∠BCD=180°.将下列推理过程补充完整:
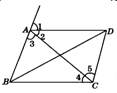
(1)∵∠1=∠ABC(已知),
∴_____∥______
(_______________________________________)
(2)∵∠3=∠5(已知),
∴_____∥______,
(_________________________________________)
(3)∵_______∥________,(已知),
∴∠ABC+∠BCD=180°
(__________________________________________)
25.如图,已知AB∥CD,试再添上一个条件,使∠1=∠2成立(要求给出两个答案).
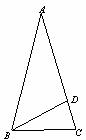
26.如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC.
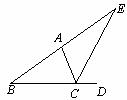
27.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
证明:∠BAC>∠B
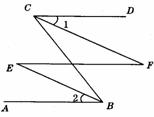
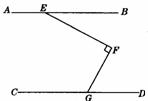
28.如图,点E在AB上,点G在CD上,EF⊥GF于F.∠AEF=150°,∠DGF=60°,试判断AB和CD的位置关系,并说明理由.
五、探究题(本题满分10分)
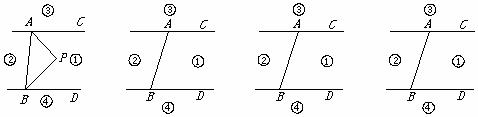
29.如图,直线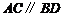 ,连接
,连接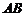 ,直线
,直线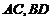 及线段
及线段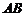 把平面分成①,②,③,④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接
把平面分成①,②,③,④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接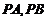 ,构成
,构成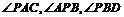 三个角.(提示:有公共顶点的两条重合的射线所组成的角是0°角)
三个角.(提示:有公共顶点的两条重合的射线所组成的角是0°角)
(1)当动点P落在第①部分时,请你判断: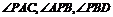 三个角之间的关系,并说明理由;
三个角之间的关系,并说明理由;
(2)当动点P落在第②部分时,以上三角的关系是否仍然成立?(直接回答成立或不成立)
(3)当动点P落在第③部分时,全面探究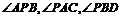 之间的关系,并写出动点P的具体位置和相应的结论,选择其中一种结论说明理由.
之间的关系,并写出动点P的具体位置和相应的结论,选择其中一种结论说明理由.