2009年临沂市中考模拟数学试题(三)
说明:本试题满分120分,考试时间120分钟。
第Ⅰ卷(选择题 共42分)
一、选择题(本大题共14小题,每小题3分,共42分。在每小题所给的四个选项中,只有一项是符合题目要求的。)
1.下列各组数中,互为相反数的是
A.2和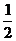 B.-2和
B.-2和 C.-2和
C.-2和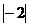 D.
D.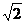 和
和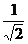
2.在“2008北京”奥运会国家体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为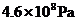 的钢材,那么
的钢材,那么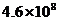 的原数为
的原数为
A.4600000 B.
3.下列各式计算正确的是
A.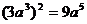 B.
B.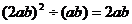
C.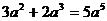 D.
D.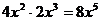
4.如下图,已知直线AB∥CD,∠C=115°,∠A=25°,则∠E=
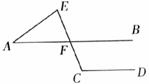
A.70° B.80° C.90° D.100°
5.化简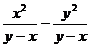 的结果是
的结果是
A.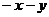 B.
B.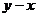 C.
C.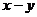 D.
D.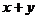
6.下列计算错误的是
A.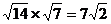 B.
B.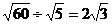
C.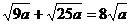 D.
D.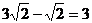
7.若关于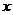 的不等式组
的不等式组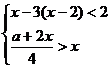 有解,则实数
有解,则实数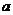 的取值范围是
的取值范围是
A.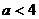 B.
B.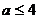 C.
C. D.
D.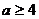
8.如下图是某几何体的三视图及相关数据,则判断正确的是
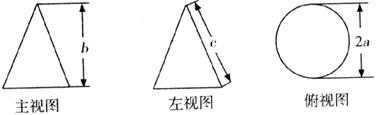
A.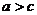 B.
B.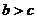 C.
C. D.
D.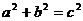
9.下列说法正确的是
A.买一张彩票就中大奖是不可能事件
B.天气预报称:“明天下雨的概率是90%”,则明天一定会下雨
C.要了解夏季冷饮市场上冰淇淋的质量情况,可以采取抽样调查的方式进行
D.掷两枚普通的正方体骰子,点数之积是奇数与点数之积是偶数出现的机会相同
10.已知如下图,四边形ABCD是平行四边形,下列结论中不正确的是
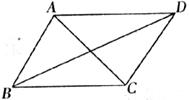
A.当AB=BC时,它是菱形 B.当∠ABC=90°时,它是矩形
C.当AC⊥BD时,它是菱形 D.AC=BD时,它是正方形
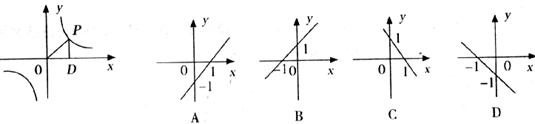
11.如下图,点P为反比例函数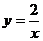 上的一动点,作PD⊥
上的一动点,作PD⊥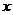 轴,垂足为点D,△POD的面积为
轴,垂足为点D,△POD的面积为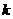 ,则函数
,则函数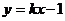 的图像是
的图像是
12.有一矩形纸片ABCD,其中AD=
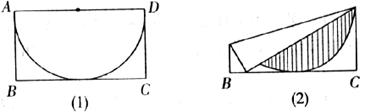
A.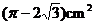 B.
B.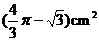
C.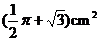 D.
D.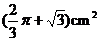
13.在拼图游戏中,从图(1)的四张纸片中任取两张纸片,能拼成“小房子”(如图(2))的概率是

A.1 B.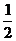 C.
C.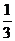 D.
D.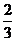
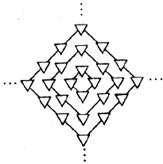
14.如下图中的三角形是有规律地从里到外逐层排列的,设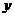 为第
为第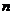 层(
层(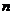 为正整数)三角形的个数,则下列函数关系式中正确的是
为正整数)三角形的个数,则下列函数关系式中正确的是
A. B.
B.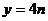 C.
C.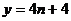 D.
D.
第Ⅱ卷(非选择题 共78分)
二、填空题(本大题共5小题,每小题3分,共15分)
15.分解因式: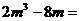 __________。
__________。
16.已知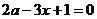 ,
,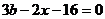 ,且
,且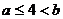 ,则
,则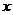 的取值范围是_________。
的取值范围是_________。
17.某超市1月份的营业额为200万元,1月、2月、3月的营业额共1000万元,若平均每月的增长率为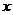 ,则由题意列方程应为__________。
,则由题意列方程应为__________。
18.如下图,正方形ABCD的边长为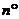 后得正方形AEFG边EF与CD交于点D,重叠部分(四边形AEOD)的面积为
后得正方形AEFG边EF与CD交于点D,重叠部分(四边形AEOD)的面积为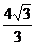 cm2,则旋转的角度
cm2,则旋转的角度 。
。
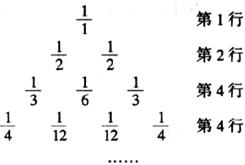
19.将杨辉三角中的每一个数都换成分数,得到一个如下图所示的分数三角形,称为莱布尼茨三角形,如果用有序实数对(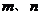 )表示第
)表示第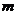 行,从左到右第
行,从左到右第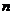 个数,如(4,3)表示分数
个数,如(4,3)表示分数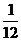 ,那么(9,2)表示的分数是__________。
,那么(9,2)表示的分数是__________。
三、开动脑筋,你一定能做对!(本大题共3小题,共20分)
20.(本小题满分6分)
把一副扑克牌中的3张黑桃牌(它们的正面牌面数字分别是3,4,5)洗匀后正面朝下放在桌面上。
(1)如果从中随机抽取一张牌,那么牌面数字是4的概率是多少?
(2)小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽取一张牌,记下牌面数字后放回,洗匀后正面朝下。再由小李随机抽出一张牌,记下牌面数字。当2张牌面数字相同时,小王赢;当2张牌面数字不相同时,小李赢,现请你利用树形图或列表法分析游戏规则双方是否公平?并说明理由。
21.(本小题满分7分)
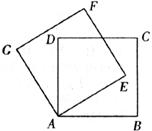
如下图,四边形ABCD,DEFG都是正方形,连结AE,CG,AE与CG相交于点M,与DG相交于点H,CG与AD相交于点N。
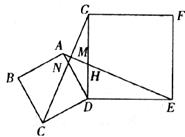
(1)线段AE和CG有怎样的关系?并加以证明;
(2)AN?DN=CN?MN
22.(本小题满分7分)
某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完。由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了1元,他用1500元所购该书数量比第一次多10本。当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书,试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱了赔多少?若赚钱了,赚多少?
四、认真思考,你一定能成功!(本大题共2小题,共19分)
23.(本小题满分9分)
已知:如下图,△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=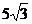 ,请求出:
,请求出:

(1)∠AOC的度数;
(2)劣弧AC的长(结果保留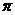 );
);
(3)线段AD的长(结果保留根号)。
24.(本小题满分6分)
某化工厂现有甲种原料7t,乙种原料5t。现计划用这两种原料生产两种不同的化工产品A和B共8t,已知生产每吨A、B产品所需的甲、乙两种原料如下表:
甲原料
乙原料
A产品
0.6t
0.8t
B产品
1.1t
o.4t
销售A、B两种产品获得的利润分别为0.45万元ㄍ吨,0.5万元ㄍ吨,若设化工厂生产A产品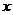 t,且销售这两种产品所获得的总利润为
t,且销售这两种产品所获得的总利润为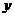 万元。
万元。
(1)求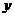 与
与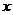 的函数关系式,并求出
的函数关系式,并求出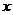 的取值范围;
的取值范围;
(2)化工厂生产A产品多少吨时,所获得的利润最大?最大利润是多少?
五、相信自己,加油呀!(本大题共2小题,共24分)
25.(本小题满分12分)
如下图,等腰梯形ABCD中,AB=9,CD=9,∠C=60°,动点P从点C出发沿CD方向向点D运动,动点Q同时以相同的速度从点D出发沿DA方向向终点A运动,其中一个动点达到端点时,另一个动点也随之停止运动。
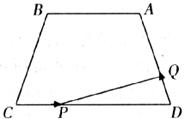
(1)求AD的长;
(2)设CP=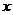 ,问当
,问当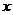 为何值时,△PDQ的面积达到最大,并求出最大值。
为何值时,△PDQ的面积达到最大,并求出最大值。
(3)探究:在BC边上是否存在点肘使得四边形PDQM是菱形?若存在,请找出点M并求出BM的长;若不存在,请说明理由。
26.(本小题满分12分)
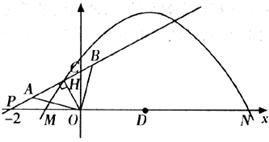
如下图,抛物线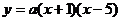 与
与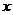 轴的交点为M、N,直线
轴的交点为M、N,直线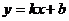 与
与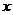 轴交于点P(-2,0)与
轴交于点P(-2,0)与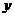 轴交于点C。若A、B两点在直线
轴交于点C。若A、B两点在直线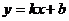 上,且AD=BO=
上,且AD=BO=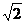 ,AO⊥BO,D为线段MN的中点,OH为Rt△OPC斜边上的高。
,AO⊥BO,D为线段MN的中点,OH为Rt△OPC斜边上的高。
(1)OH的长度等于__________;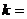 __________,
__________,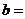 __________。
__________。
(2)是否存在实数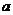 ,使得抛物线
,使得抛物线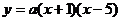 上有一点E,满足以D、N、E为顶点的三角形与△AOB相似?若不存在,说明理由,若存在,求所有符合条件的抛物线的解析式,同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由),并进一步探索对符合条件的每一个点E,直线NE与直线AB的交点G是否满足
上有一点E,满足以D、N、E为顶点的三角形与△AOB相似?若不存在,说明理由,若存在,求所有符合条件的抛物线的解析式,同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由),并进一步探索对符合条件的每一个点E,直线NE与直线AB的交点G是否满足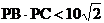 ,写出探索过程。
,写出探索过程。