2009年临沂市中考模拟数学试题(二)
说明:本试题满分120分,考试时间120分钟。
第Ⅰ卷(选择题 共42分)
一、选择题(本大题共14小题,每小题3分,共42分。在每小题所给的四个选项中,只有一项是符合题目要求的。)
1.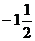 的倒数是
的倒数是
A.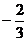 B.
B.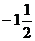 C.
C.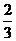 D.
D.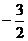
2.继短信之后,音乐类产品逐步成为我国手机户的最爱和移动通信新的增长点,目前中国移动彩铃用户已超过40000000,占中国移动4亿用户总数的近10%,40000000用科学记数法可表示为
A.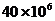 B.
B.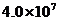 C.
C.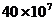 D.
D.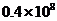
3.下列运算正确的是
A.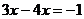 B.
B.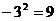
C.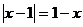
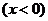 D.
D.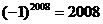
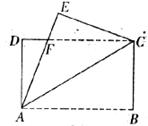
4.如下图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于
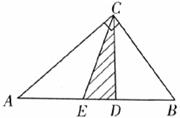
A.25° B.30° C.45° D.60°
5.函数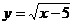 的自变量的取值范围是
的自变量的取值范围是
A.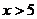 B.
B. C.
C.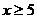 D.
D.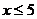
6.若M(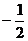 ,
,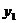 ),N(
),N(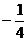 ,
, ),P(
),P(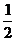 ,
,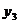 )三点都在函数
)三点都在函数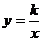 (
(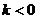 )的图像上,则
)的图像上,则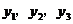 的大小关系为
的大小关系为
A.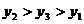 B.
B.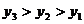 C.
C.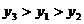 D.
D.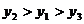
7.若不等式组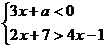 的解集为
的解集为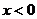 ,则
,则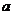 的取值范围为
的取值范围为
A.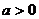 B.
B.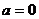 C.
C.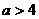 D.
D.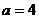
8.下列说法正确的是
A.随机事件发生的可能性是50%
B.检测某城市的空气质量,采用抽样调查
C.一组数据2,3,3,6,8,5的众数与中位数都是3
D.若甲组数据的方差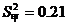 ,已组数据的方差
,已组数据的方差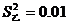 ,则甲组数据比乙组数据稳定
,则甲组数据比乙组数据稳定
9.由大小相同的正方体木块堆成的几何体的三视图如下图所示,则该几何体中正方体木块的个数是
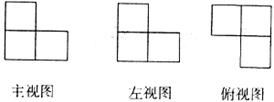
A.6个 B.5个 C.4个 D.3个
10.矩形纸片ABCD中,AB=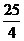 cm,则AD的长为
cm,则AD的长为
A.
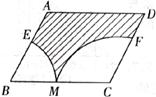
11.如下图:平行四边形ABCD中,BC=12,M为BC中点,M到AD的距离为8,若分别以B、C为圆心,BM长为半径画弧,交AB、CD于E、F两点,则图中斜线区域面积为
A.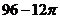 B.
B.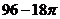 C.
C.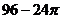 D.
D.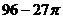
12.如下图,在菱形ABCD中,∠A=135°,AB=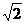 ,以点C为圆心的弧EF分别与AB、CD相切于点C,H,与BC、CD分别交于点E、F,用扇形CEF作成圆锥侧面,则圆锥的高为
,以点C为圆心的弧EF分别与AB、CD相切于点C,H,与BC、CD分别交于点E、F,用扇形CEF作成圆锥侧面,则圆锥的高为
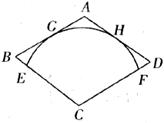
A.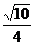 B.
B.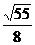 C.
C.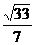 D.
D.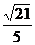
13.如下图,直线AB与半径为2的⊙O相切于点C,D是⊙O上的一点,且∠EDC=30°,弦EF∥AB,则EF的长度为
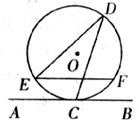
A.2 B.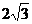 C.
C.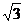 D.
D.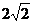
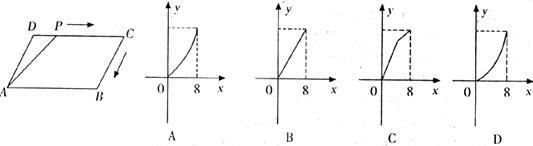
14.如下左图,在□ABCD中,∠DAB=60°,AB=5,BC=3,点P从起点D出发,沿DC、CB向终点B匀速运动,设点P所走过的路程为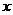 ,点P所经过的线段与线段AD、AP所围成的图形的面积为
,点P所经过的线段与线段AD、AP所围成的图形的面积为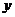 ,
,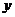 随
随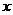 的变化而变化,在下列图像中,能正确反映
的变化而变化,在下列图像中,能正确反映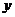 与
与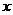 的函数关系的是
的函数关系的是
第Ⅱ卷 (非选择题 共78分)
二、填空题(本大题共5小题,每小题3分,共15分)
15.计算: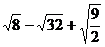 的结果是__________。
的结果是__________。
16.为解决老百姓看病准的问题,决定下调药品的价格,某利药品经过两次降价,由每盒72元调至56元,若每次平均降价的百分率均为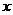 ,由题意可列方程为__________。
,由题意可列方程为__________。
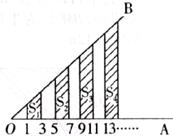
17.如下图,∠AOB=45°,过OA上到点O距离分别为1,3,5,7,9,11,……的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为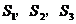 ,
,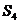 ,……,观察图中的规律,求出第10个黑色梯形的面积
,……,观察图中的规律,求出第10个黑色梯形的面积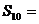 __________。
__________。
18.一根蜡烛经凸透镜成一实像,物距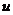 ,像距
,像距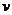 和凸透镜的焦距
和凸透镜的焦距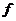 ,满足关系,且
,满足关系,且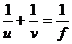 ,用
,用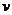 ,
,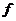 表示的物距
表示的物距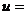 __________。
__________。
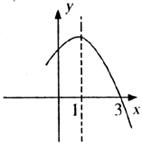
19.已知二次函数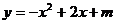 的部分图像如下图所示,则关于
的部分图像如下图所示,则关于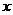 的一元二次方程
的一元二次方程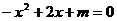 的解为__________。
的解为__________。
三、开动脑筋,你一定能做对!(本大题共3小题,共20分)
20.(本小题满分6分)
某种子培育基地用A、B、C、D四种型号的小麦种子共2000粒进行发芽实验,从中选出发芽率高的种子进行推广,通过实验得知,C型号种子的发芽率为95%,根据实验数据绘制了图(1)和图(2)两幅尚不完整的统计图。
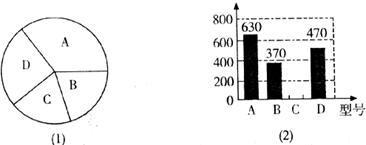
(1)D型号种子的粒数是__________。
(2)请你将图(2)的统计图补充完整;
(3)通过计算说明,应选哪一个型号的种子进行推广;
(4)若将所有已发芽的种子放到一起,从中随机取一粒,求取到B型号发芽种子的概率。
21.(本小题满分7分)
已知:如下图,在Rt△ABC 4中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A。
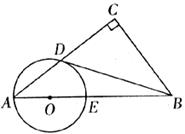
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD┱AO=8┱5,BC=2,求BD的长。
22.(本小题满分7分)
如下图,一次函数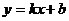 的图像与反比例函数
的图像与反比例函数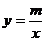 的图像相交于A、B两点。
的图像相交于A、B两点。
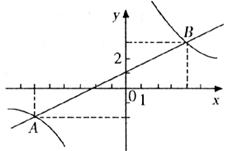
(1)根据图像,分别写出A、B的坐标;
(2)求出两函数解析式;
(3)根据图像回答:当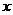 为何值时,一次函数值大于反比例数的函数值。
为何值时,一次函数值大于反比例数的函数值。
四、认真思考,你一定能成功(本大题共2小题,共19分)
23.(本小题满分9分)
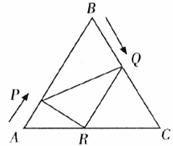
如图,已知△ABC是边长为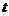 (s),解答下列问题:
(s),解答下列问题:
(1)当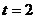 时,判断BPQ的形状,并说明理由;
时,判断BPQ的形状,并说明理由;
(2)设△BPQ的面积为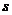 (cm2),求
(cm2),求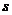 与
与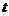 的函数关系式;
的函数关系式;
(3)作QR∥BA交AC于点R,连接PR,当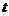 为何值时,△APR∽△PRQ?
为何值时,△APR∽△PRQ?
24.(本小题满分10分)
在“5?12大地震”灾民安置工作中,某企业接到一批生产甲种板材
(1)已知该企业安排140人生产这两种板材,每人每天能生产甲板材
(2)某灾民安置点计划用该企业生产的这批板材搭建A、B两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材,已知建一间A型板房和一问B型板房所需板材及能安置的人数如下表所示:
板房型号
甲种板材
乙种板材
安置人数
A型板房
5
B型板房
8
问:这400间板房最多能安置多少灾民?
五、相信自己,加油呀!(本大题共2小题,共24分)
25.(本小题满分11分)
如下图(1),△ABC的边BC在直线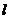 上,AC⊥BC,且AC=BC;△EFD的边FP也在直线
上,AC⊥BC,且AC=BC;△EFD的边FP也在直线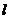 上,边EF与边AC重合,且EF=FD。
上,边EF与边AC重合,且EF=FD。
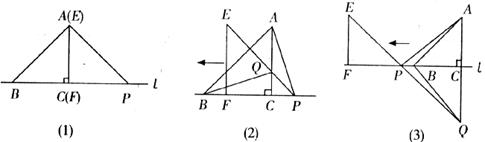
(1)如图(1)中,请你通过观察测量,猜想并写出AB与AP所满足的数量关系的位置关系;
(2)将△EFP沿直线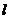 向左平移到图(2)的位置时,EP交AC于点Q,连结AP,BQ。猜想并写出BQ和AP所满足的数量关系和位置关系,请证明你的猜想;
向左平移到图(2)的位置时,EP交AC于点Q,连结AP,BQ。猜想并写出BQ和AP所满足的数量关系和位置关系,请证明你的猜想;
(3)将△EFP沿直线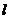 向左平移到图(3)的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ。你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由。
向左平移到图(3)的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ。你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由。
26.(本小题满分13分)
已知抛物线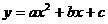 的图像交
的图像交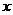 轴于点A(
轴于点A(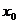 ,0)和点B(2,0),与
,0)和点B(2,0),与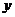 轴的正半轴交于点C,其对称轴是直线
轴的正半轴交于点C,其对称轴是直线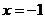 ,
,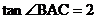 ,点A关于
,点A关于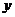 轴的对称点为点D。
轴的对称点为点D。
(1)确定A、C、D三点的坐标;
(2)求过B、C、D三点的抛物线的解析式;
(3)若过点(0,3)且平行于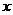 轴的直线与(2)小题中所求抛物线交于M、N两点,以MN 为一边,抛物线上任一点P(
轴的直线与(2)小题中所求抛物线交于M、N两点,以MN 为一边,抛物线上任一点P(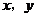 )为顶点作平行四边形,若平行四边形的面积为S,写出S关于P点纵坐标
)为顶点作平行四边形,若平行四边形的面积为S,写出S关于P点纵坐标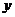 的函数解析式;
的函数解析式;
(4)当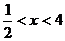 时,(3)小题中平行四边形的面积是否有最大值,若有,请求出;若无,请说明理由。
时,(3)小题中平行四边形的面积是否有最大值,若有,请求出;若无,请说明理由。