2009年南充市高中阶段学校招生统一考试
数学试卷
(满分100分,考试时间90分钟)
一、细心选一选(本大题共8个小题,每小题3分,共24分)每小题下面都有代号为A、B、C、D的四个选项,其中只有一个选项是正确的,请把正确选项的代号填在该题后面的括号内.填写正确记3分,不填、填错或填出的代号超过一个均记0分.
1.计算 的结果是( )
的结果是( )
A. B.
B.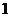 C.
C.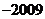 D.
D.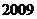
2.在平面直角坐标系中,点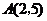 与点B关于
与点B关于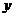 轴对称,则点B的坐标是( )
轴对称,则点B的坐标是( )
A.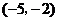 B.
B.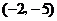 C.
C. D.
D.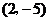
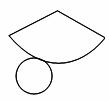
3.某物体的展开图如图,它的左视图为( )

4.方程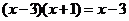 的解是( )
的解是( )
A. B.
B.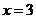 C.
C.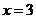 或
或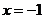 D.
D.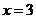 或
或
5.已知一组数据2,1,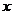 ,7,3,5,3,2的众数是2,则这组数据的中位数是(
)
,7,3,5,3,2的众数是2,则这组数据的中位数是(
)
A.2
B.
6.化简 的结果是( )
的结果是( )
A.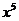 B.
B.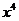 C.
C.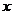 D.
D.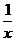
7.抛物线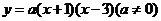 的对称轴是直线(
)
的对称轴是直线(
)
A.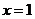 B.
B.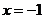 C.
C.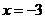 D.
D.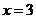
8.如图,AB是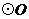 的直径,点C、D在
的直径,点C、D在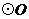 上,
上,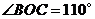 ,
,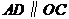 ,则
,则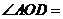 ( )
( )

A.70° B.60° C.50° D.40°
二、认真填一填(本大题共4个小题,每小题3分,共12分)请将答案直接填写在题中横线上.
9.不等式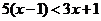 的解集是 .
的解集是 .
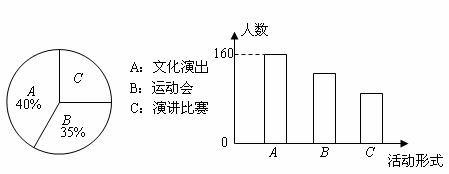
10.某校为了举办“庆祝建国60周年”的活动,调查了本校所有学生,调查的结果如图所示,根据图中给出的信息,这所学校赞成举办演讲比赛的学生有 人.
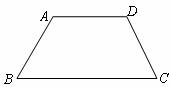
11.如图,等腰梯形ABCD中,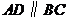 ,
,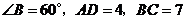 ,则梯形ABCD的周长是 .
,则梯形ABCD的周长是 .
12.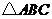 中,
中, ,以点B为圆心、
,以点B为圆心、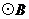 ,则边AC所在的直线与
,则边AC所在的直线与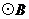 的位置关系是
.
的位置关系是
.
三、(本大题共2个小题,每小题6分,共12分)
13.计算: .
.
14.化简: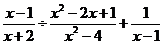 .
.
四、(本大题共2个小题,每小题6分,共12分)
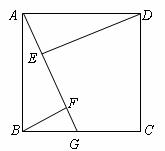
15.如图,ABCD是正方形,点G是BC上的任意一点,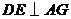 于E,
于E,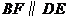 ,交AG于F.
,交AG于F.
求证: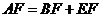 .
.
16.甲口袋中装有两个相同的小球,它们分别写有1和2;乙口袋中装有三个相同的小球,它们分别写有3、4和5;丙口袋中装有两个相同的小球,它们分别写有6和7.从这3个口袋中各随机地取出1个小球.
(1)取出的3个小球上恰好有两个偶数的概率是多少?
(2)取出的3个小球上全是奇数的概率是多少?
五、(本大题共2个小题,每小题8分,共16分)
17.在达成铁路复线工程中,某路段需要铺轨.先由甲工程队独做2天后,再由乙工程队独做3天刚好完成这项任务。已知乙工程队单独完成这项任务比甲工程队单独完成这项任务多用2天,求甲、乙工程队单独完成这项任务各需要多少天?
18.如图,在平面直角坐标系中,已知点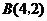 ,
,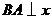 轴于A.
轴于A.
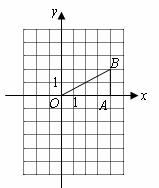
(1)求 的值;
的值;
(2)将点B绕原点逆时针方向旋转90°后记作点 ,求点
,求点 的坐标;
的坐标;
(3)将 平移得到
平移得到 ,点A的对应点是
,点A的对应点是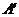 ,点
,点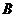 的对应点
的对应点 的坐标为
的坐标为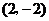 ,在坐标系中作出
,在坐标系中作出 ,并写出点
,并写出点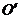 、
、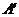 的坐标.
的坐标.
六、(本大题8分)
19.某电信公司给顾客提供了两种手机上网计费方式:
方式A以每分钟0.1元的价格按上网时间计费;方式B除收月基费20元外,再以每分钟0.06元的价格按上网时间计费.假设顾客甲一个月手机上网的时间共有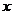 分钟,上网费用为
分钟,上网费用为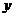 元.
元.
(1)分别写出顾客甲按A、B两种方式计费的上网费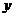 元与上网时间
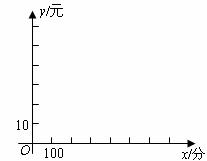
元与上网时间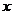 分钟之间的函数关系式,并在下图的坐标系中作出这两个函数的图象;
分钟之间的函数关系式,并在下图的坐标系中作出这两个函数的图象;
(2)如何选择计费方式能使甲上网费更合算?
七、(本大题8分)
20.如图,半圆的直径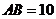 ,点C在半圆上,
,点C在半圆上,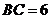 .
.
(1)求弦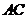 的长;
的长;
(2)若P为AB的中点,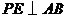 交
交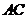 于点E,求
于点E,求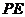 的长.
的长.

八、(本大题8分)
21.如图,已知正比例函数和反比例函数的图象都经过点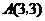 .
.
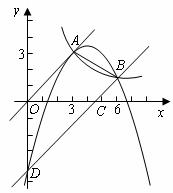
(1)求正比例函数和反比例函数的解析式;
(2)把直线OA向下平移后与反比例函数的图象交于点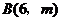 ,求
,求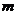 的值和这个一次函数的解析式;
的值和这个一次函数的解析式;
(3)第(2)问中的一次函数的图象与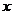 轴、
轴、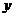 轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
(4)在第(3)问的条件下,二次函数的图象上是否存在点E,使四边形OECD的面积 与四边形OABD的面积S满足:
与四边形OABD的面积S满足: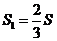 ?若存在,求点E的坐标;若不存在,请说明理由.
?若存在,求点E的坐标;若不存在,请说明理由.