2008-2009学年度潍坊市昌邑初中学段第一学期八年级期末考试
数学试卷
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请将正确答案的序号填写在题后的括号内。每小题3分。共45分)
1.在实数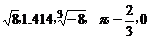 ,中无理数有( )
,中无理数有( )
A.1个 B.2个 C.3个 D.4个
2.估计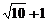 的值是( )
的值是( )
A.在2和3之间 B.在3和4之间 C.在4和5之间 D.在5和6之间
3.把代数式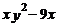 分解因式,结果正确的是( )
分解因式,结果正确的是( )
A.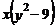 B.
B.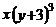 C.
C. D.
D.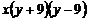
4.下列运算正确的是( )
A.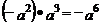 B.
B.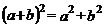
C.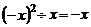 D.
D.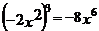
5.如下图,在平行四边形ABCD中,AE平分∠BAD交DC边于点E,DF⊥AE于F,已知∠ADF=50°,∠C的度数为( )
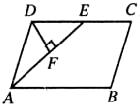
A.85° B.80° C.75° D.70°
6.现有两根铁棒,它们的长分别为
A.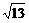 米 B.
米 B.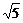 米 C.
米 C.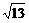 米或
米或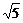 米 D.
米 D.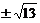 米
米
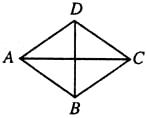
7.如下图所示,在菱形ABCD中,不一定成立的是( )
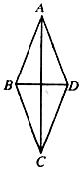
A.四边形ABCD是平行四边形 B.AC⊥BD
C.△ABD是等边三角形 D.∠CAB=∠CAD
8.如下图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是( )
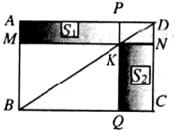
A.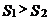 B.
B.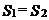 C.
C.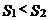 D.无法确定
D.无法确定
9.矩形、菱形、正方形都具有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线平分一组对角 D.对角线互相垂直
10.正方形的边长为 ,则它的对角线的交点到边的距离为( )
,则它的对角线的交点到边的距离为( )
A.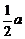 B.
B.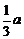 C.
C.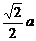 D.
D.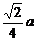
11.如果线段AB是线段CD经过平移得到的,那么线段AC与BD的关系是( )
A.相交 B.平行 C.平行且相等 D.以上都不对
12.如下图,在长方形ABCD中,AB=2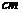 ,AD=4
,AD=4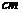 ,E、F分别为AD、BC的中点,分别以C,F为圆心、2
,E、F分别为AD、BC的中点,分别以C,F为圆心、2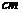 为半径画圆把长方形分成三个部分,则图中两个阴影部分的面积为( )
为半径画圆把长方形分成三个部分,则图中两个阴影部分的面积为( )
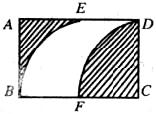
A.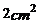 B.
B. C.
C.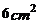 D.无法确定
D.无法确定
13.下列说法错误的是( )
A.图形在平移过程中,图形上的每一点都移动了相同的距离
B.等边三角形既是轴对称图形,又是旋转对称图形
C.图形在旋转过程中,图形上的每一点都绕旋转中心转过了同样长的路程
D.中心对称图形的对称中心只有一个,而轴对称图形的对称轴可能不只一条
14.用两个完全相同的直角三角形拼下列图形:①平行四边形;②矩形;③菱形;④正方形;⑤等腰三角形;⑥等边三角形。一定可以拼成的图形是( )
A.①②③ B.①②⑤ C.①④⑤ D.②⑤⑥
15.如下图,四边形ABCD是菱形,对角线AC=8,BD=6,BE⊥CD,则BE的长是( ).

A.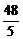 B.
B.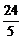 C.
C.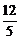 D.以上都不对
D.以上都不对
二、填空题(每小题3分,共27分)
1.若一个数的平方根是3,则这个数是_______;若一个数的平方是3,则这个数是________.
2.若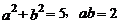 ,则
,则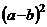 =_________.
=_________.
3.如下图,在多边形ABCDEF中,AB=5 ,BC=6
,BC=6 ,则多边形的周长为_________.
,则多边形的周长为_________.

4.给出下列图形:①线段 ②平行四边形 ③圆 ④矩形 ⑤等腰梯形.其中,旋转对称图形有____________________ (只填序号)
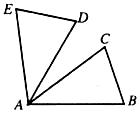
5.如下图,已知∠CAB=30°,△ABC绕着点A旋转55°后能与△ADE重合,则∠CAD=________.
6.若平行四边形ABCD的周长是28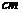 ,O是对角线AC、BD的交点,且△AOB的周长比△BOC的周长多2
,O是对角线AC、BD的交点,且△AOB的周长比△BOC的周长多2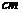 ,则AB=________,AD=________.
,则AB=________,AD=________.
7.如下图,△ABD≌△ACE,且∠A=20°,∠C=65°,则∠ADB=________.
8.如下图,菱形ABCD的对角线AC=24,BD=10,则菱形的周长 =________.
=________.
9.如下图,E为正方形ABCD的边BC延长线上的点,且CE=AC,连接AE,则∠E=________.
三、解答题(解答应写出必要的计算过程、推演步骤或文字说明)
1.(7分)如下图,矩形ABCD的两对角线相交于点O,∠AOD=120°,AC=6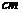 ;
;
(1)判断△AOB的形状;(2)求矩形ABCD各边的长.

2.(6分)先化简,再求值: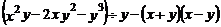 其中,
其中,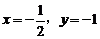 .
.
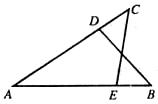
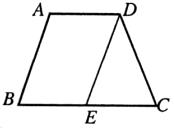
3.(7分)如下图,在等腰梯形ABCD中,AD∥BC,AB∥DE,∠C=60°,AD=7,AB=9,求梯形的周长.
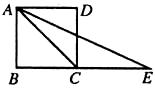
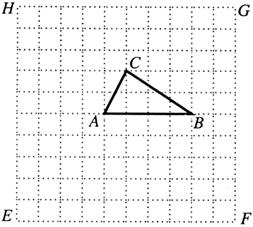
4.(8分)如下图,在一个10×10的正方形EFGH网格中有一个△ABC.
(1)在网格中画出△ABC向下平移4个单位得到的△ .
.
(2)在网格中画出△ABC绕C点逆时针方向旋转90°得到的△AB
5.(10分)如图1,在四边形ABCD中,对角线AC⊥BD,垂足为P,试说明S四边形ABCD= AC?BD
AC?BD
解:因为AC⊥BD
所以S△ACD= AC?PD,S△ACB=
AC?PD,S△ACB= AC?BP
AC?BP
所以S四边形ABCD= S△ACD+S△ACB= AC?PD+
AC?PD+ AC?BP=
AC?BP= AC(PD+PB)=
AC(PD+PB)= AC?BD
AC?BD
解答问题:
(1)上述证明得到的性质可叙述为:
(2)如图2,已知等腰梯形ABCD中,AD∥BC,对角线AC⊥BD且相交于点P,AP=2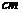 ,BP=5
,BP=5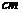 ,利用上述性质求梯形的面积.
,利用上述性质求梯形的面积.

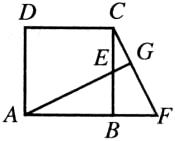
6.(10分)如图所示,已知正方形ABCD,E为BC上任意一点,延长AB至F,使BF=BE,AE的延长线交CF于G,试说明(1)AE=CF;(2)AG⊥CF.