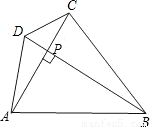
摘要：所以S△ACD=AC?PD.S△ACB=AC?BP
网址：http://m.1010jiajiao.com/timu_id_749491[举报]
阅读材料：
如图（1），在四边形ABCD中，对角线AC⊥BD，垂足为点P．求证：S四边形ABCD=
AC•BD；
证明：∵AC⊥BD，
∴
∴S四边形ABCD=S△ACD+S△ACB=AC•PD+AC•BP
=AC（PD+PB）=AC•BD
解答问题：
（1）上述证明得到的性质可叙述为______
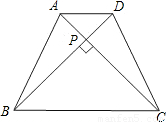
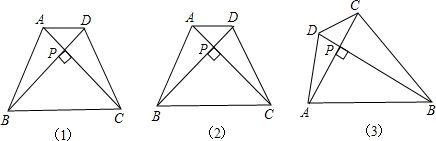
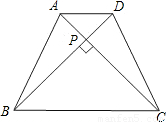
（2）已知：如图（2），在等腰梯形ABCD中，AD∥BC，对角线AC⊥BD，且相交于点P，AD=3cm，BC=7cm，利用上述性质求梯形的面积．
（3）如图（3），用一块面积为800cm2的等腰梯形彩纸做风筝，并用两根竹条作梯形的对角线固定风筝，对角线恰好互相垂直，问竹条的长是多少？
查看习题详情和答案>>
（2004•湟中县）阅读材料：如图在四边形ABCD中，对角线AC⊥BD，垂足为P．
求证：S四边形ABCD=
AC•BD．
证明：AC⊥BD?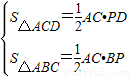
∴S四边形ABCD=S△ACD+S△ACB=
AC•PD+
AC•BP
=
AC（PD+PB）=
AC•B D
解答问题：
（1）上述证明得到的性质可叙述为______；
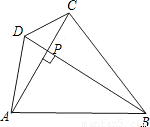
（2）已知：如图，等腰梯形ABCD中，AD∥BC，对角线AC⊥BD且相交于点P，AD=3cm，BC=7cm，利用上述的性质求梯形的面积．
查看习题详情和答案>>
求证：S四边形ABCD=
AC•BD．证明：AC⊥BD?
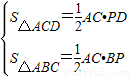
∴S四边形ABCD=S△ACD+S△ACB=
AC•PD+AC•BP=
AC（PD+PB）=AC•B D解答问题：
（1）上述证明得到的性质可叙述为______；
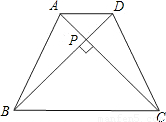
（2）已知：如图，等腰梯形ABCD中，AD∥BC，对角线AC⊥BD且相交于点P，AD=3cm，BC=7cm，利用上述的性质求梯形的面积．
查看习题详情和答案>>
阅读材料：如下图（1）所示，在四边形ABCD中，对角线AC⊥BD于P，求证：S四边形ABCD=
AC·BD。
证明：AC⊥BD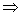
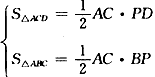
∴S四边形ABCD=S△ACD+S△ACB=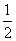
AC·PD+
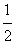AC·BP=
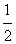AC·（PD+PB）=
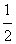AC·BD。
AC·BD。证明：AC⊥BD
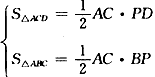
∴S四边形ABCD=S△ACD+S△ACB=
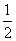AC·PD+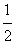AC·BP=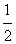AC·（PD+PB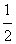）=AC·BD。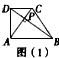
（1）上述证明得到的性质可叙述为：____；
（2）已知：上图（2）所示，等腰梯形ABCD中，AD∥BC，AC⊥BD于P，AD=3cm，BC=7cm，利用上述的性质求梯形的面积。
查看习题详情和答案>>
（2）已知：上图（2）所示，等腰梯形ABCD中，AD∥BC，AC⊥BD于P，AD=3cm，BC=7cm，利用上述的性质求梯形的面积。
AC•BD．
AC•PD+
AC•BP
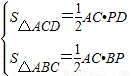
AC（PD+PB）=
AC•B D
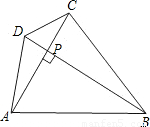
AC•BD．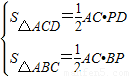
AC•PD+
AC•BP
AC（PD+PB）=
AC•B D
