摘要：5．如图1.在四边形ABCD中.对角线AC⊥BD.垂足为P.试说明S四边形ABCD=AC?BD解:因为AC⊥BD
网址：http://m.1010jiajiao.com/timu_id_749490[举报]
阅读材料：
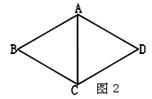
如图(1)，在四边形ABCD中，对角线AC⊥BD，垂足为P，求证：S四边形ABCD＝
AC·BD．
证明：∵AC⊥BD 
∴
∴S四边形ABCD＝S△ACD＋S△ABC＝AC·PD＋AC·PB＝AC(PD＋PB)＝AC ·BD
解答问题：
(1)上述证明得到的性质可叙述为： ▲
(2)已知：如图(2)，等腰梯形ABCD中，AD∥BC，对角线AC⊥BD且相交于点P，AD＝3cm，BC＝7cm，利用上述的性质求梯形的面积．
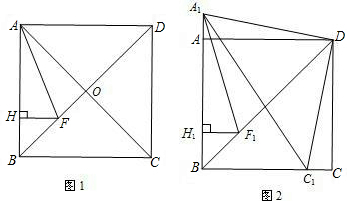
如图1，在正方形ABCD中，对角线AC与BD相交于点O，AF平分∠BAC，交BD于点F．
（1）求证：DF=AD；
（2）过点F作FH⊥AB，垂足为点H，求证：FH+
AC=AD；
（3）如图2，将∠ADC绕顶点D旋转一定的角度后，DC边所在的直线与BC边交于点C1（不与点B重合），DA边所在的直线与BA边的延长线交于点A1． A1F1平分∠BA1C1，交BD于点F1，过点F1作F1H1⊥AB，垂足为H1，试猜想F1H1、
A1C1与AD三者之间的数量关系，并证明你的猜想．
查看习题详情和答案>>
（1）求证：DF=AD；
（2）过点F作FH⊥AB，垂足为点H，求证：FH+
| 1 |
| 2 |
（3）如图2，将∠ADC绕顶点D旋转一定的角度后，DC边所在的直线与BC边交于点C1（不与点B重合），DA边所在的直线与BA边的延长线交于点A1． A1F1平分∠BA1C1，交BD于点F1，过点F1作F1H1⊥AB，垂足为H1，试猜想F1H1、
| 1 |
| 2 |
查看习题详情和答案>>
（2013•济南）（1）如图1，在△ABC和△DCE中，AB∥DC，AB=DC，BC=CE，且点B，C，E在一条直线上．
求证：∠A=∠D．
（2）如图2，在矩形ABCD中，对角线AC，BD相交于点O，AB=4，∠AOD=120°，求AC的长．
查看习题详情和答案>>
求证：∠A=∠D．
（2）如图2，在矩形ABCD中，对角线AC，BD相交于点O，AB=4，∠AOD=120°，求AC的长．
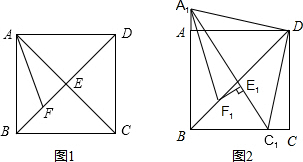如图1，在正方形ABCD中，对角线AC与BD相交于点E，AF平分∠BAC，交BD于点F．