2008-2009学年度潍坊市高密初中学段第一学期九年级期末考试
数学试卷
(时间:90分钟)
一、选择题(共12个小题,每小题3分,共36分)
1.下列各式中属于最简二次根式的是( )
A. B.
B.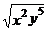 C.
C.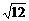 D.
D.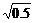
2.下列说法正确的是( ).
A.“明大降雨的概率是80%”表示明天有80%的时间降雨
B.“抛一枚硬币正面朝上的概率是
C.“彩票中奖的概率是1%”表示买100张彩票一定会中奖
D.“抛一枚正方体骰子朝正面的数为奇数的概率是
3.已知二次根式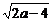 与
与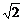 是同类二次根式,则
是同类二次根式,则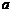 的值可以是( )
的值可以是( )
A.5 B.
4.如图,在△ABC中,∠C=90°,AC=8 ,AB的垂直平分线MN交AC于D,连结BD,若
,AB的垂直平分线MN交AC于D,连结BD,若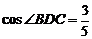 ,则BC的长是( )
,则BC的长是( )
A.4 B.6
B.6 C.8
C.8 D.10
D.10
5.一个布袋里装有3个红球、2个白球,每个球除颜色外均相同,从中任意摸出一个球,则摸出的球是红球的概率是( ).
A. B.
B. C.
C.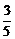 D.
D.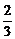
6.如果方程组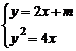 只有一个实数解,那么
只有一个实数解,那么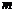 的值为( )
的值为( )
A. B.
B.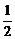 C.
C.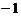 D.0
D.0
7.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中△ABC相似的是( )

8.如图,已知∠ACB=∠CBD=90°,BC=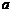 ,AC=
,AC=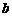 ,当CD=( )时,△CDB∽△ABC.
,当CD=( )时,△CDB∽△ABC.
A.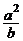 B.
B.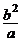 C.
C.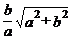 D.
D.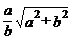
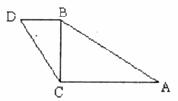
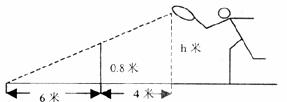
9.如图,小明在打网球时,使球恰好能打过网,而且落点恰好在离网6米的位置上,则球拍击球的高度h为( )米。.
A.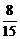 B.1 C.
B.1 C.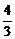 D.
D.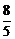
10.坡角为30°的斜坡上两树间的水平距离为2米,则两树间的坡面距离为( )
A.4米 B. 米 C.
米 C.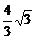 米 D.
米 D. 米
米
11.如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE:EB=4:1,EF⊥AC于F,连结FB,则tan∠CFB的值等于( )
A.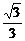 B.
B.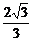 C.
C.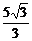 D.
D.

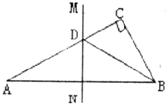
12.如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
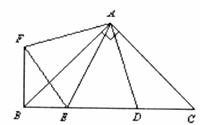
①△AED≌△AEF; ②△ABE∽△ACD; ③BE+DC=DE; ④BE2+DC2=DE2
其中正确的是
A.②④ B.①④ C.②③ D.①③
二、填空题(共8个小题,每个小题3分,共24分)
13.一元二次方程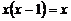 的解是________.
的解是________.
14.若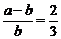 ,则
,则 =________.
=________.
15.某山路的路面坡度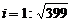 ,沿此山路向上前进200
,沿此山路向上前进200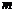 ,升高了________
,升高了________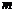 .
.
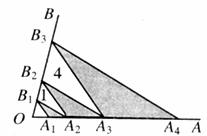
16.如图,点A1、A2、A3、A4在射线OA上,点B1、B2、B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2、△A3B2B3的面积分别为1、4,则图中三个阴影三角形面积之和为________.
17.有大小、形状、颜色完全相同的5个乒乓球,每个球上分别标有数字1、2、3、4、5中的一个,将这5个球放入不透明的袋中搅匀,如果不放回的从中随机连续抽取两个,则这两个球上的数字之和为偶数的概率是________.
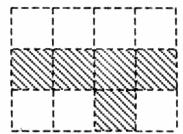
18.如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分.现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是________.
19.已知关于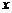 的方程
的方程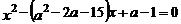 两个根是互为相反数,则
两个根是互为相反数,则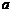 的值为____.
的值为____.
20.如图,小明同学从A地沿北偏两60°方向走100米到B地,再从B地向正南方向走200米到达C地,此时小明同学离A地________米.

三、解答题(共6个小题,满分60分)
21.(本题满分8分)
计算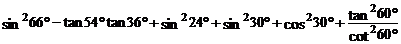
22.(本题满分10分)
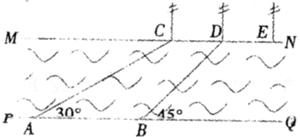
如图,河流的两岸PQ、MN互相平行,河岸MN上有一排间隔为50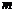 的电线杆C、D、E、…,某人在河岸PQ的A处测得∠CAQ=30°,然后沿河岸走了110
的电线杆C、D、E、…,某人在河岸PQ的A处测得∠CAQ=30°,然后沿河岸走了110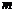 到达B处,测得∠DBQ=45°,求河流的宽度(结果可带根号)
到达B处,测得∠DBQ=45°,求河流的宽度(结果可带根号)
23.(本题满分10分)
如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,
(1)求证:AC=BD;
(2)若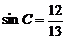 ,BC=12,求AD的长.
,BC=12,求AD的长.

24.(本题满分10分)
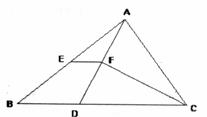
如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连结EF.
(1)求证:EF∥BC.
(2)若四边形BDFE的面积为6,求△ABD的面积.
25.(10分)有三张卡片(背面完全相同)分别写有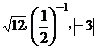 ,把它们背面朝上洗匀后,小军从中抽取一张,记下这个数后放回洗匀,小明又从中抽出一张.
,把它们背面朝上洗匀后,小军从中抽取一张,记下这个数后放回洗匀,小明又从中抽出一张.
(1)两人抽取的卡片上都是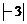 的概率是________.
的概率是________.
(2)李刚为他们俩设定了一个游戏规则:若两人抽取的卡片上两数之积是有理数,则小军获胜,否则小明获胜,你认为这个游戏规则对谁有利?请用列表法或树状图进行分析说明.
26.课题研究(12分)
(1)如图(1),我们已经学习了直角三角形中的边角关系,在Rt△ACD中sin∠A=_____,所以CD=________,而S△ABC=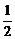 AB?CD,于是可将三角形面积公式变形,得S△ABC=_____.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.
AB?CD,于是可将三角形面积公式变形,得S△ABC=_____.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.
(2)如图(2),在△ABC中,CD⊥AB于D,∠ACD=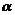 ,∠DCB=
,∠DCB=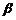 .
.
∵S△ABC=S△ADC+ S△BDC,由公式①,得
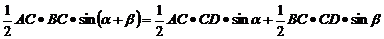
即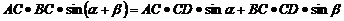 ②
②
请你利用直角三角形边角关系,消去②中的AC、BC、CD,将得到新的结论.并写出解决过程.
(3)利用(2)中的结论,试求sin75°和sin105°的值,并比较其大小。