网址:http://m.1010jiajiao.com/timu_id_749389[举报]
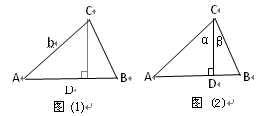
(1)如图(1),我们已经学习了直角三角形中的边角关系,在Rt△ACD中,sin∠A=
| 1 |
| 2 |
(2)如图(2),在△ABC中,CD⊥AB于D,∠ACD=α,∠DCB=β.
∵S△ABC=S△ADC+S△BDC,由公式①,得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
请你利用直角三角形边角关系,消去②中的AC、BC、CD,将得到新的结论.并写出解决过程.
(3)利用(2)中的结论,试求sin75°和sin105°的值,并比较其大.
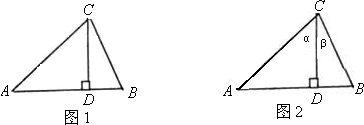 查看习题详情和答案>>
查看习题详情和答案>>
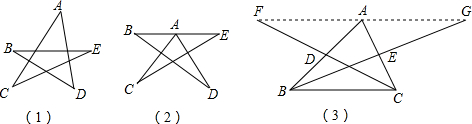
(1)图(1)中是一个五角星形状,则∠A+∠B+∠C+∠D+∠E=
(2)图(1)中的点A向下移到BE上时(如图(2))五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化?说明你的结论的正确性;
(3)如图(3),在△ABC中,CD、BE分别是AB、AC边上的中线,延长CD到F,使FD=CD,延长BE到G,使EG=BE,F、A、G三点是否在一条直线上?说说你的理由.
如图(1),由直角三角形边角关系,可将三角形面积公式变形,
即: 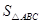 =
=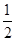 AB·CD,
AB·CD,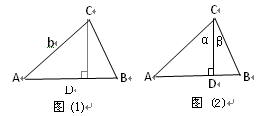
在Rt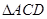 中,
中,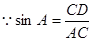 ,
,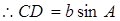
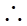
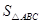 =
=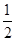 bc·sin∠A.
bc·sin∠A.
即 三角形的面积等于两边之长与夹角正弦之积的一半.
如图(2),在 ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
∵ 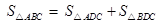 , 由公式①,得
, 由公式①,得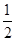 AC·BC·sin(α+β)=
AC·BC·sin(α+β)= 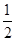 AC·CD·sinα+
AC·CD·sinα+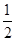 BC·CD·sinβ,
BC·CD·sinβ,
即 AC·BC·sin(α+β)= AC·CD·sinα+BC·CD·sinβ
请你利用直角三角形边角关系,消去②中的AC、BC、CD,只用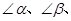
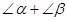 的正弦或余弦函数表示(直接写出结果).
的正弦或余弦函数表示(直接写出结果).
【小题1】(1)______________________________________________________________
【小题2】(2)利用这个结果计算: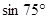 =_________________________
=_________________________
即:
 =
= AB·CD,
AB·CD,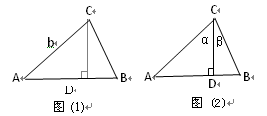
在Rt
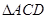 中,
中,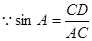 ,
,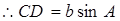
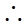
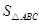 =
=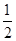 bc·sin∠A.
bc·sin∠A.即 三角形的面积等于两边之长与夹角正弦之积的一半.
如图(2),在
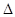 ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.∵
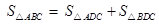 , 由公式①,得
, 由公式①,得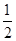 AC·BC·sin(α+β)=
AC·BC·sin(α+β)= 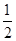 AC·CD·sinα+
AC·CD·sinα+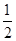 BC·CD·sinβ,
BC·CD·sinβ,即 AC·BC·sin(α+β)= AC·CD·sinα+BC·CD·sinβ
请你利用直角三角形边角关系,消去②中的AC、BC、CD,只用

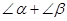 的正弦或余弦函数表示(直接写出结果).
的正弦或余弦函数表示(直接写出结果).【小题1】(1)______________________________________________________________
【小题2】(2)利用这个结果计算:
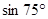 =_________________________
查看习题详情和答案>>
=_________________________
查看习题详情和答案>>
如图(1),由直角三角形边角关系,可将三角形面积公式变形,
即: ![]() =
=![]() AB·CD,
AB·CD,
在Rt![]() 中,
中,![]() ,
,
![]()
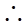
![]() =
=![]() bc·sin∠A.
bc·sin∠A.
即 三角形的面积等于两边之长与夹角正弦之积的一半.
如图(2),在![]() ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
∵ ![]() , 由公式①,得
, 由公式①,得
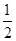 AC·BC·sin(α+β)=
AC·BC·sin(α+β)=![]() AC·CD·sinα+
AC·CD·sinα+![]() BC·CD·sinβ,
BC·CD·sinβ,
即 AC·BC·sin(α+β)= AC·CD·sinα+BC·CD·sinβ
请你利用直角三角形边角关系,消去②中的AC、BC、CD,只用![]()
![]() 的正弦或余弦函数表示(直接写出结果).
的正弦或余弦函数表示(直接写出结果).
1.(1)______________________________________________________________
2.(2)利用这个结果计算:![]() =_________________________
=_________________________
查看习题详情和答案>>