2008-2009学年度枣庄市滕州第一学期九年级期末考试
数学试卷
一、选择题:每题3分,共45分。
1.下列方程中,是一元二次方程的是
A.x=2y-3 B.2(x+1)=
2.到三角形各顶点的距离相等的点是三角形
A.三条角平分线的交点 B.三条高的交点
C.三边的垂直平分线的交点 D.三条中线的交点
3.甲、乙两地相距

4.下列命题中,不正确的是
A.顺次连结菱形各边中点所得的四边形是矩形
B.有一个角是直角的菱形是正方形
C.对角线相等且垂直的四边形是正方形
D.有一个角是600的等腰三角形是等边三角形
5.电影院呈阶梯或下坡形状的主要原因是
A.为了美观 B.减小盲区 C.增大盲区 D.盲区不变
6.如下图所示,在平行四边形ABCD中,CE是∠DCB的平分线,F是AB的中点,AB=6,BC=4.则AE:EF:FB=( )
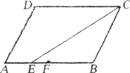
A.1:2:3 B.2:l:3
C.3:2:1 D.3:l:2
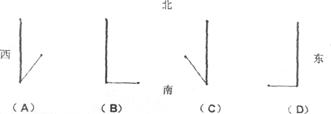
7.若点(3,4)在反比例函数y=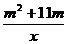 的图象上,则此反比例函数必经过点
的图象上,则此反比例函数必经过点
A.(2,6) B.(2,一6) C.(4,一3) D(3,一4)
8.若菱形的较长对角线为
A.
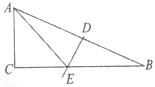
9.如下图,在Rt△ABC中,∠C=900,∠B=22.50,DE垂直平分AB交BC于E,若BE=2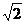 .则AC=
.则AC=
A.1 B.
10.在△ABC中,a=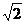 ,b=
,b=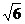 ,c=2
,c=2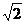 ,则最大边上的中线长为
,则最大边上的中线长为
A.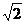 B.
B. C.2 D.以上都不对
C.2 D.以上都不对
11.一件产品原来每件的成本是100元,由于连续两次降低成本,现在的成本是81元,则平均每次降低成本
A.8.5% B.9% C.9.5%. D.10%
12.函数y=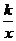 (k≠0)的图象过点(2,一2),则此函数的图象在平面直角坐标系中的
(k≠0)的图象过点(2,一2),则此函数的图象在平面直角坐标系中的
A.第一、三象限 B.第三、四象限 C.第一、二象限 D.第二、四象限
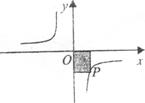
13.如下图,P是反比例函数的图象上的一点,过点P分别向x轴、y轴作垂线,所得到的图中的阴影部分的面积为6,则该反比例函数的表达式为
A.y=-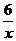 B.y=
B.y=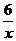

 C.y=-
C.y=-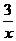 D.y=
D.y=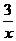
14.如下图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在奇数上的概率是

A. B.
B. C.
C. D.
D.
15.若点A(-2,y1 )、B(-1,y2)、C(1,y3)在反比例函数y=-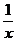 的图像上,则
的图像上,则
A.y1> y2> y3 B.y 3> y2> y1 C.y2>y1>y3 D.y1> y2> y 3
二、填空题:(每题3分,共27分)
16.已知关于x的一元二次方程(a-1)x2―x+a2―1=0的一个根是0,那么a的值为______。
17.小亮和他弟弟在阳光下散步,小亮的身高为1.75米,他的影子长2米。若此时他的弟弟的影子长为1.6米,则弟弟的身高为____________米。
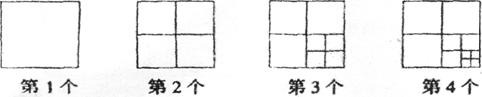
18.观察下列一组图形,根据其变化规律,可得第8个图形中所有正方形的个数为_____个。
19.如下图:(A) (B) (C) (D)是一天中四个不同时刻的木杆在地面上的影子,将它们时间后顺序进行排列,为_________________;
20.已知名x2+4x一2=0,那么3x2+12x+2000的值为____________。
21.下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是图形
_____________________(请填图形下面的代号)。

22.在一个可以改变容积的密闭容器内,装有一定质量的某种气体,当改变容积V时,气体的密度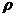 也随之改变.在一定范围内,密度
也随之改变.在一定范围内,密度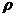 是容积V的反比例函数.当容积为5m3时密度是l.4kg/m3,则
是容积V的反比例函数.当容积为5m3时密度是l.4kg/m3,则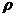 与V的函数关系式为______________。
与V的函数关系式为______________。
23.如下图,将矩形纸片ABCD沿AE向上折叠,使点B落在DC边上的F点处.若△AFD的周长为9,△ECF的周长为3,则矩形ABCD的周长为_______________________________。

24.若点(m,n)在反比例函数y=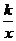 (k≠0)的图象上,其中m,n是方程x2一2x一8=0的两根,则k=___________________。
(k≠0)的图象上,其中m,n是方程x2一2x一8=0的两根,则k=___________________。
三.解答题:共6小题,满分48分,解答应写出文字说明.证明过程或演算步骤。
25.(6分)
关于x的一元二次方程kx2―6x一4=0。
求:(1)当k为何值时,方程有解;(2)当k为何值时,方程无解。
26.(6分)
如下图,小明和小芳在大门外听到大门内小颖说话的声音,但都看不到小颖.请你用阴影画出小颖的可能活动范围。

27.(6分)
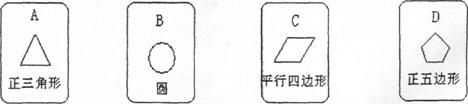
有四张背面相同的纸牌A,B,C,D其正面分别画有四个不同的几何图形如下图所示,小华将这四张牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张。
(1)用列表法(或树状图)表示两次摸牌所有可能出现的结果(纸牌可用A,B,C,D表示)。
(2)求摸出两张牌面图形都是中心对称图形的纸牌的概率。
28.(8分)如下图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽。

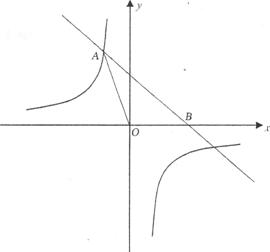
29.(本小题8分)如下图,已知直线y= 一x+4与反比例函数)y= 的图象相交于点
的图象相交于点
A(一2,a),并且与x轴相交于点B。
(1)求a的值;
(2)求反比例函数的表达式;
(3)求 AOB的面积。
AOB的面积。
30.(14分)
如下图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP。

(1)在图中是否存在两个全等的三角形,若存在请写出这两个三角形并证明;若不存在请说明理由。
(2)若(1)中存在,这两个三角形通过旋转能够互相重合吗?若重合请说出旋转的过程;若不重合请说明理由。
(3)PB与BE有怎样的位置关系,说明理由。
(4)若PA=1,PB=2,∠APB=135 0,求AE的值。