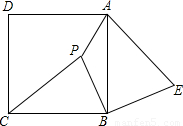
摘要：30． 如下图.P是正方形ABCD内一点.在正方形ABCD外有一点E.满足∠ABE=∠CBP.BE=BP.
网址：http://m.1010jiajiao.com/timu_id_749123[举报]
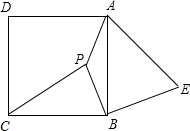如图，P是正方形ABCD内一点，在正方形ABCD外有一点E，满足∠ABE=∠CBP，BE=BP．（1）在图中是否存在两个全等的三角形，若存在请写出这两个三角形并证明；若不存在请说明理由；
（2）若（1）中存在，这两个三角形通过旋转能够互相重合吗？若重合请说出旋转的过程；若不重合请说明理由；
（3）PB与BE有怎样的位置关系，说明理由；
（4）若PA=1，PB=2，∠APB=135°，求AE的值． 查看习题详情和答案>>
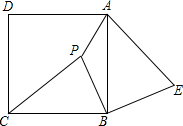已知：如图，P是正方形ABCD内一点，在正方形ABCD外有一点E，满足∠ABE=∠CBP，BE=BP．（1）求证：△CPB≌△AEB；
（2）求证：PB⊥BE；
（3）若PA：PB=1：2，∠APB=135°，求cos∠PAE的值． 查看习题详情和答案>>
已知，如图，P是正方形ABCD内一点，在正方形ABCD外有一个点E，满足∠ABE=∠CBP，BE=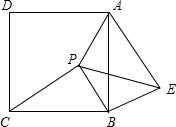
BP
（1）求证：△CPB≌△AEB；
（2）求证：PB⊥BE；
（3）若∠APB=135°，判断△PAE形状，并説明你的理由． 查看习题详情和答案>>
BP（1）求证：△CPB≌△AEB；
（2）求证：PB⊥BE；
（3）若∠APB=135°，判断△PAE形状，并説明你的理由． 查看习题详情和答案>>
21、已知：如图，P是正方形ABCD内一点，在正方形ABCD外有一点E，满足∠ABE=∠CBP，BE=BP．