2007年临沂市郯城中考模拟试题二
数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分l20分。考试时间l20分钟。
第Ⅰ卷(选择题 共39分)
一、选择题(共13小题,每小题3分,共39分,每小题只有一个选项是符合题意的,请把唯一正确答案的代号涂在答题卡上)
1.下列计算正确的是( )
A. B.
B. C.
C. D.
D.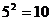
2.已知 是方程
是方程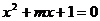 的一个实数根,则
的一个实数根,则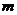 的值是(
)
的值是(
)
A.0 B.
3.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A.小明的影子比小强的影子长 B.小明的影长比小强的影子短
C.小明的影子和小强的影子一样长 D.无法判断谁的影子长
4.初三的几位同学拍了一张合影作留念,已知冲一张底片需要0.80元,洗一张相片需要0.35元。在每位同学得到一张相片、共用一张底片的前提下,平均每人分摊的钱不足0.5元,那么参加合影的同学人数( )
A.至多6人 B.至少6人 C.至多5人 D.至少7人
 5.数学老师布置10道选择题作为课堂练习,课代表将全班同学的答题情况绘制成条形统计图(如右图),根据此图可知,每位同学答对的题数所组成样本的中位数和众数分别为(
)
5.数学老师布置10道选择题作为课堂练习,课代表将全班同学的答题情况绘制成条形统计图(如右图),根据此图可知,每位同学答对的题数所组成样本的中位数和众数分别为(
)
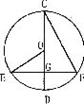
A.8,8 B.8,9
C.9,9 D.9,8
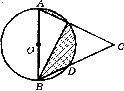 6.如右图,AB是⊙O的,直径点D、E是半圆的三等分点,AE,BD的延长线交于点C。若CE=2,则图中阴影部分的面积是( )
6.如右图,AB是⊙O的,直径点D、E是半圆的三等分点,AE,BD的延长线交于点C。若CE=2,则图中阴影部分的面积是( )
A. B.
B.
C.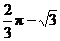 D.
D.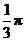
7.如右图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )
A.80°
 B.50°
B.50°
C.40°
D.20°
8.如图1,在边长为a的正方形中剪去一个边长为b的小正形(a>b),把剩下部分拼成一个梯形(如图2),利用这两幅图形面积,可以验证的公式是( )

A.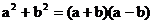 B.
B.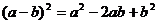
C.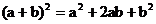 D.
D.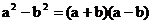
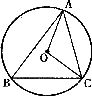 9.如图,⊙O是△ABC的外接圆,连接OA、OC,⊙O的半径R=2,
9.如图,⊙O是△ABC的外接圆,连接OA、OC,⊙O的半径R=2,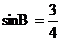 ,则弦AC的长为( )
,则弦AC的长为( )
A.3 B.
C.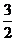 D.
D.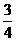
10.根据下列表格的对应值:

3.23
3.24
3.25
3.26

-0.06
-0.02
0.03
0.09
判断方程 =0(a≠0,a,b,C为常数)一个解
=0(a≠0,a,b,C为常数)一个解 的范围是( ) A.
的范围是( ) A.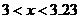 B.
B.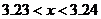
C. D.
D.
11.某学习小组在讨论“变化的鱼”时,知道下图中的大鱼与小鱼是位似图形,若小鱼上的 点P(a,b)对应大鱼上的点Q,则点Q的坐标为( )

A.(-
12.若用(1)、(2)、(3)、(4)四幅图像分别表示变量之间的关系,
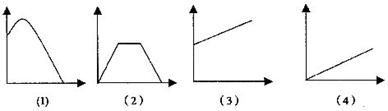
请按图像所给顺序,将下面的(a)、(b)、(c)、(d)对应排序
(a)小车从光滑的斜面上滑下(小车的速度与时间的关系)
(b)一个弹簧不挂重物到逐渐挂重物(弹簧长度与所挂重物的重量的关系)
(c)运动员推出去的铅球(铅球的高度与时间的关系)
(d)小杨从A到B后,停留一段时间,然后按原速度返回(路程与时间的关系)
正确的顺序是( )
A.(c)(d)(b)(a) B.(a)(b)(c)(d)
C.(b)(c)(a)(d) D.(d)(a)(c)(b)
13.现有2008年奥运会福娃卡片20张,其中贝贝6张,京京5张,欢欢4张,迎迎3张,妮妮2张,每张卡片大小、质地均匀相同,将画有福娃的一面朝下反扣在桌子上,从中随机抽取一张,抽到京京的概率是( )
A. B.
B. C.
C. D.
D.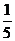
第Ⅱ卷(非选择题 共81分)
二、填空题(每小题3分,共有7个小题,本题满分21分)
14.如图,在等腰△ABC中,∠C=90°,BC=

 15.不等式组
15.不等式组 的解集为
。
的解集为
。
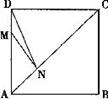
16.如右图,正方形ABCD的边长为8,M在AD上,且DM=2,N是AC上一动点,则DN+MN的最小值为 。
 17.按一定的规律排列的一列数依次为:
17.按一定的规律排列的一列数依次为: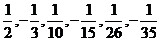 … …,按此规律排列下去,这列数中的第8个数是
。
… …,按此规律排列下去,这列数中的第8个数是
。
18.如右图,P是∠AOB的平分线上一点,C、D分别是OB、OA上的点,若要使PD=PC,只需添加一个条件即可。请写出这一个条件: 。
19.如图:矩形AOCB的两边OC、OA分别位于x轴、y轴上,点B的坐标为B(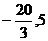 ),D是AB边上的一点。将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图像上,那么该函数的解析式是
。
),D是AB边上的一点。将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图像上,那么该函数的解析式是
。

20.直角坐标系中直线AB交x轴,y轴于点A(4,0)与B(0,-3),现有一半径为1的动圆的圆心位于原点处,以每秒l个单位的速度向右作平移运动,则经过 秒后动圆与直线AB相切。
三、解答题(本大题7小题,共60分)
21.(本题满分8分)
(1)
(2)化简: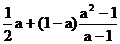
22.(9分)
将一条长为
(1)要使这两个正方形的面积之和等于
(2)两个正方形的面积之和可能等于l
23.(本题6分)
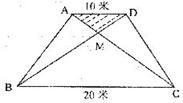
某社区拟筹资金2000元,计划在一块上、下底分别是l
24.(9分)
如图,作△ABC的中线AD,并将△ADC绕点D旋转l80°,那么点C与点B重合,点A转到A′点,不难发现AC=A′B,AD=A′D,BD=DC,如果知道AB=

(1)请你探索中线AD的取值范围是多少
(2)如图梯形ABCD中,AD∥BC,M是AD的中点,N是BC的中点,如果AB=10,CD=6,则MN的取值范围是 。
25.(8分)
如图,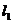 、
、 分别表示一种白炽灯和一种节能灯的费用
分别表示一种白炽灯和一种节能灯的费用 (费用=灯的售价+电费,单位:元)与照明时间
(费用=灯的售价+电费,单位:元)与照明时间 (小时)的函数图像,假设两种灯的使用寿命都是2000小时,照明效果一样。
(小时)的函数图像,假设两种灯的使用寿命都是2000小时,照明效果一样。
(1)根据图像分别求出 、
、 的函数关系式;
的函数关系式;
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2500小时,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程。)
26.(10分)
如图,已知AB是⊙O的直径,AC是⊙O的弦,点D是弧ABC中点,弦DE⊥AB,垂足为F,DE交AC与点G。

(1)图中有哪些相等的线段?(要求:不再标注其他字母,找结论的过程中所作的辅助线不能出线在结论中,不写出推理过程)
(2)若过点E作⊙O的切线ME,交AC的延长线于点M(请补完整图形)。试问:ME=MG是否成立?若成立,请证明;若不成立,请说明理由。
(3)在满足第(2)问的条件下,已知AF=3,FB=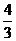 ,求AG与GM的比。(第(1)的结论可直接利用)
,求AG与GM的比。(第(1)的结论可直接利用)
27.(10分)
如图,已知抛物线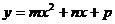 与
与 关于
关于 轴对称,与
轴对称,与 轴交于点M,与
轴交于点M,与 轴交于点A和B。
轴交于点A和B。

(1)求出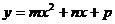 的解析式,试猜想出与一般形式抛物线
的解析式,试猜想出与一般形式抛物线 关于
关于 轴对称的二次函数解析式(不要求证明)。
轴对称的二次函数解析式(不要求证明)。
(2)A,B的中点是点C,求sin∠CMB。