摘要：(1)请你探索中线AD的取值范围是多少(2)如图梯形ABCD中.AD∥BC.M是AD的中点.N是BC的中点.如果AB=10.CD=6.则MN的取值范围是 .
网址：http://m.1010jiajiao.com/timu_id_677828[举报]
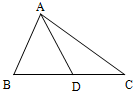
9、如图，已知：AD是△ABC的中线．（1）画出与△ADC关于点D成中心对称的三角形；
（2）找出与AC相等的线段；
（3）探索：三角形中AB与AC的和与中线AD之间的关系，并说明理由；
（4）若AB=5，AC=3，则线段AD的取值范围是多少？
如图，△ABC中，点D是BC中点，连接AD并延长到点E，连接BE．（1）若要使△ACD≌△EBD，应添上条件：
AC∥BE
AC∥BE
；（2）证明上题；
（3）在△ABC中，若AB=5，AC=3，可以求得BC边上的中线AD的取值范围是AD＜4．请看解题过程：由△ACD≌△EBD得：AD=ED，BE=AC=3，因此AE＜AB+BE，即AE＜8，而AD=
| 1 | 2 |
1
1
．
如图，△ABC中，点D是BC中点，连接AD并延长到点E，连接BE．（1）若要使△ACD≌△EBD，应添上条件：
AD=DE
AD=DE
；（2）证明：
（3）在△ABC中，若AB=5，AC=3，可以求得BC边上的中线AD的取值范围是AD＜4．请看解题过程：由△ACD≌△EBD得：AD=ED，BE=AC=3，因此AE＜AB+BE，即AE＜8，而AD=
| 1 | 2 |
1
1
．所以AD的取值范围是1＜AD＜4
1＜AD＜4
．
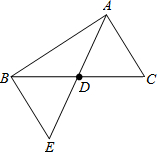如图，△ABC中，点D是BC中点，连接AD并延长到点E，连接BE．
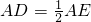，则AD＜4．请参考上述解题方法，求AD＞______．