摘要:18.如右图.P是∠AOB的平分线上一点.C.D分别是OB.OA上的点.若要使PD=PC.只需添加一个条件即可.请写出这一个条件: .
网址:http://m.1010jiajiao.com/timu_id_677817[举报]
如图,在平面直角坐标系中,O是坐标原点,点A、B的坐标分别为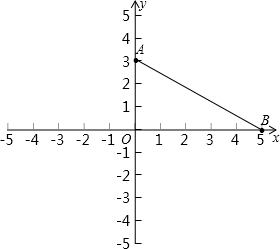 A(0,3)和B(5,0),连接AB.
A(0,3)和B(5,0),连接AB.
(1)现将△AOB绕点O按逆时针方向旋转90°,得到△COD,(点A落到点C处),请画出△COD,并求经过B、C、D三点的抛物线对应的函数关系式;
(2)将(1)中抛物线向右平移两个单位,点B的对应点为点E,平移后的抛物线与原抛物线相交于点F、P为平移后的抛物线对称轴上一个动点,连接PE、PF,当|PE-PF|取得最大值时,求点P的坐标;
(3)在(2)的条件下,当点P在抛物线对称轴上运动时,是否存在点P使△EPF为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由. 查看习题详情和答案>>
 A(0,3)和B(5,0),连接AB.
A(0,3)和B(5,0),连接AB.(1)现将△AOB绕点O按逆时针方向旋转90°,得到△COD,(点A落到点C处),请画出△COD,并求经过B、C、D三点的抛物线对应的函数关系式;
(2)将(1)中抛物线向右平移两个单位,点B的对应点为点E,平移后的抛物线与原抛物线相交于点F、P为平移后的抛物线对称轴上一个动点,连接PE、PF,当|PE-PF|取得最大值时,求点P的坐标;
(3)在(2)的条件下,当点P在抛物线对称轴上运动时,是否存在点P使△EPF为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由. 查看习题详情和答案>>
如图,在平面直角坐标系中,O是坐标原点,点A、B的坐标分别为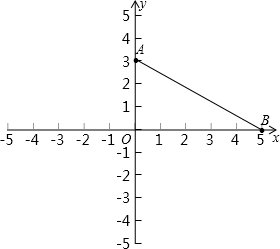 A(0,3)和B(5,0),连接AB.
A(0,3)和B(5,0),连接AB.
(1)现将△AOB绕点O按逆时针方向旋转90°,得到△COD,(点A落到点C处),请画出△COD,并求经过B、C、D三点的抛物线对应的函数关系式;
(2)将(1)中抛物线向右平移两个单位,点B的对应点为点E,平移后的抛物线与原抛物线相交于点F、P为平移后的抛物线对称轴上一个动点,连接PE、PF,当|PE-PF|取得最大值时,求点P的坐标;
(3)在(2)的条件下,当点P在抛物线对称轴上运动时,是否存在点P使△EPF为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看习题详情和答案>>
如图,在平面直角坐标系中,O是坐标原点,点A、B的坐标分别为A(0,3)和B(5,0),连接AB。
(1)现将△AOB绕点O按逆时针方向旋转90°,得到△COD(点A落到点C处),求经过B、C、D三点的抛物线的解析式;
(2)将(l)中抛物线向右平移两个单位长度,点B的对应点为点E,平移后的抛物线与抛物线相交于点F,P为平移后的抛物线对称轴上一个动点,连接PE、PF,当|PE-PF|取得最大值时,求点P的坐标;
(3)在(2)的条件下,当点P在抛物线对称轴上运动时,是否存在点P使△EPF为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由。
(1)现将△AOB绕点O按逆时针方向旋转90°,得到△COD(点A落到点C处),求经过B、C、D三点的抛物线的解析式;
(2)将(l)中抛物线向右平移两个单位长度,点B的对应点为点E,平移后的抛物线与抛物线相交于点F,P为平移后的抛物线对称轴上一个动点,连接PE、PF,当|PE-PF|取得最大值时,求点P的坐标;
(3)在(2)的条件下,当点P在抛物线对称轴上运动时,是否存在点P使△EPF为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由。
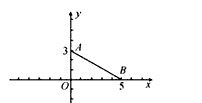
(2010•崇文区二模)如图,在平面直角坐标系中,O是坐标原点,点A、B的坐标分别为A(0,3)和B(5,0),连接AB.
(1)现将△AOB绕点O按逆时针方向旋转90°,得到△COD,(点A落到点C处),请画出△COD,并求经过B、C、D三点的抛物线对应的函数关系式;
(2)将(1)中抛物线向右平移两个单位,点B的对应点为点E,平移后的抛物线与原抛物线相交于点F、P为平移后的抛物线对称轴上一个动点,连接PE、PF,当|PE-PF|取得最大值时,求点P的坐标;
(3)在(2)的条件下,当点P在抛物线对称轴上运动时,是否存在点P使△EPF为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)现将△AOB绕点O按逆时针方向旋转90°,得到△COD,(点A落到点C处),请画出△COD,并求经过B、C、D三点的抛物线对应的函数关系式;
(2)将(1)中抛物线向右平移两个单位,点B的对应点为点E,平移后的抛物线与原抛物线相交于点F、P为平移后的抛物线对称轴上一个动点,连接PE、PF,当|PE-PF|取得最大值时,求点P的坐标;
(3)在(2)的条件下,当点P在抛物线对称轴上运动时,是否存在点P使△EPF为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
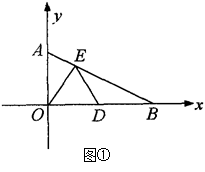
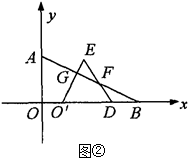
 始终相等的线段?如果存在,请指出这条线段,并加以证明;如果不存在,请说明理由.
始终相等的线段?如果存在,请指出这条线段,并加以证明;如果不存在,请说明理由.