2007年泰安市中等学校招生考试
数学试题(课改区用)
注意事项:
1.本试题分第I卷和第II卷两部分.第I卷3页为选择题,36分;第II卷8页为非选择题,84分;共120分.考试时间120分钟.
2.答第I卷前务必将自己的姓名、考号、考试科目涂写在答题卡上.考试结束,试题和答题卡一并收回.
3.第I卷每题选出答案后,都必须用2B铅笔把答题卡上对应题目的答案标号(ABCD)涂黑,如需改动,必须先用橡皮擦干净,再改涂其他答案,不能答在试卷上.
第I卷(选择题 共36分)
一、选择题(本大题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个,均记零分)
1.下列运算正确的是( )
A. B.
B.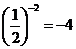 C.
C. D.
D.
2.下列运算正确的是( )
A.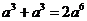 B.
B.
C. D.
D.
3.下列几何体中,其主视图、俯视图和左视图分别是右图中三个图形的是( )

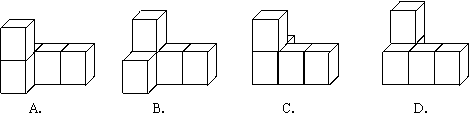
4.将 化成
化成 的形式为( )
的形式为( )
A.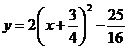 B.
B.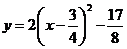
C.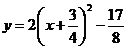 D.
D.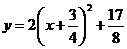
5.计算 的结果为( )
的结果为( )
A. B.
B.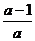 C.
C. D.
D.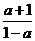
6.已知三点 ,
, ,
,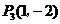 都在反比例函数
都在反比例函数 的图象上,若
的图象上,若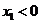 ,
,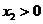 ,则下列式子正确的是( )
,则下列式子正确的是( )
A. B.
B. C.
C. D.
D.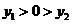
7.从标有1,2,3,4的四张卡片中任取两张,卡片上的数字之和为奇数的概率是( )
A. B.
B. C.
C.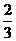 D.
D.
 8.如图,在
8.如图,在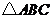 中,
中, ,
, 于
于 ,若
,若 ,
, ,则
,则 的值为( )
的值为( )
A.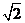 B.
B.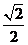 C.
C. D.
D.
 9.如图,
9.如图,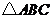 是等腰直角三角形,且
是等腰直角三角形,且 .
.
曲线 …叫做“等腰直角三角形的渐开线”,其中
…叫做“等腰直角三角形的渐开线”,其中
? ? ?
CD , DE , EF…的圆心依次按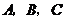 循环.
循环.
如果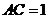 ,那么曲线
,那么曲线 和线段
和线段 围成图形
围成图形
的面积为( )
 A.
A. B.
B.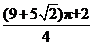
C.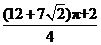 D.
D.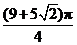
10.如图, 方格纸的两条对称轴
方格纸的两条对称轴 相交于点
相交于点 ,
,
对图 分别作下列变换:
分别作下列变换:
①先以直线 为对称轴作轴对称图形,再向上平移4格;
为对称轴作轴对称图形,再向上平移4格;
②先以点 为中心旋转
为中心旋转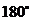 ,再向右平移1格;
,再向右平移1格;
③先以直线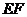 为对称轴作轴对称图形,再向右平移4格,
为对称轴作轴对称图形,再向右平移4格,
其中能将图 变换成图
变换成图 的是( )
的是( )
A.①② B.①③ C.②③ D.③
 11.如图,在正方形
11.如图,在正方形 中,
中, 是
是 的中点,
的中点, 是
是 上一点,
上一点,
且
 ,下列结论:①
,下列结论:①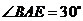 ,②
,② ,
,
③ ,④
,④ .其中正确结论的个数为( )
.其中正确结论的个数为( )
A.1 B.2
C.3 D.4
12.骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化,其体温(℃)与时间(时)之间的关系如图所示.若 (℃)表示0时到
(℃)表示0时到 时内骆驼体温的温差(即0时到
时内骆驼体温的温差(即0时到 时最高温度与最低温度的差).则
时最高温度与最低温度的差).则 与
与 之间的函数关系用图象表示,大致正确的是( )
之间的函数关系用图象表示,大致正确的是( )


 |
第II卷(非选择题 共84分)
注意事项:
1.答卷前将密封线内的项目填写清楚.
2.第II卷共8页,用蓝黑钢笔或圆珠笔直接答在试卷上.
 二、填空题(本大题共7小题,满分21分.只要求填写最后结果,每小题填对得3分)
二、填空题(本大题共7小题,满分21分.只要求填写最后结果,每小题填对得3分)
13.方程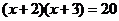 的解是 .
的解是 .
14.如图, 和
和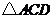 是
是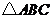 分别沿着
分别沿着
边翻折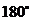 形成的,若
形成的,若 ,则
,则 的度数是 .
的度数是 .
 15.若关于
15.若关于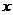 的不等式组
的不等式组 有解,则实数
有解,则实数 的取值范围是 .
的取值范围是 .
16.如图,⊙M与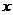 轴相交于点
轴相交于点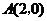 ,
, ,与
,与 轴相切于点
轴相切于点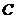 ,则圆心
,则圆心 的坐标是
.
的坐标是
.
17.如图,图①,图②,图③,……是用围棋棋子摆成的一列具有一定规律的“山”字.则第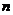 个“山”字中的棋子个数是 .
个“山”字中的棋子个数是 .
 |

18.如图,一游人由山脚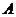 沿坡角为
沿坡角为 的山坡
的山坡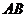 行走
行走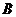 ,再由
,再由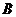 沿山坡
沿山坡 行走
行走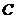 ,若在山顶
,若在山顶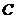 处观测到景点
处观测到景点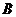 的俯角为
的俯角为 ,则山高
,则山高 等于 (结果用根号表示)
等于 (结果用根号表示)
19.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密).已知加密规则为:明文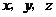 对应密文
对应密文 .例如:明文1,2,3对应密文8,11,9.当接收方收到密文12,17,27时,则解密得到的明文为 .
.例如:明文1,2,3对应密文8,11,9.当接收方收到密文12,17,27时,则解密得到的明文为 .
三、解答题(本大题共7小题,满分63分.解答应写出必要的文字说明、证明过程或推演步骤)
20.(本小题满分6分)
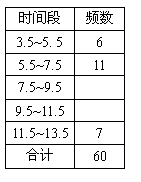 某中学为了解毕业年级800名学生每学期参加社会实践活动的时间,随机对该年级60名学生每学期参加社会实践活动的时间(单位:天)进行了统计(统计数据取整数),整理后分成5组,绘制成频数分布表和频数分布直方图(部分)如右图.
某中学为了解毕业年级800名学生每学期参加社会实践活动的时间,随机对该年级60名学生每学期参加社会实践活动的时间(单位:天)进行了统计(统计数据取整数),整理后分成5组,绘制成频数分布表和频数分布直方图(部分)如右图.
(1)补全频数分布表和频数分布直方图;
 (2)请你估算这所学校该年级的学生中,
(2)请你估算这所学校该年级的学生中,
每学期参加社会实践活动的时间大于7天
的约有多少人?
21.(本小题满分8分)
如图,在梯形 中,
中,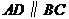 ,对角线
,对角线 平分
平分 ,
, 的平分线
的平分线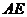 交
交 于
于 分别是
分别是 的中点.
的中点.
(1)求证: ;
;
(2)当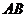 与
与 满足怎样的数量关系时,
满足怎样的数量关系时, ?并说明理由.
?并说明理由.
 |
22.(本小题满分9分)
某书店老板去图书批发市场购买某种图书.第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书数量比第一次多10本.当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
23.(本小题满分9分)
如图,在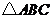 中,
中, ,以
,以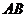 为直径的圆
为直径的圆 交
交 于点
于点 ,交
,交 于点
于点 ,过点
,过点 作
作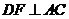 ,垂足为
,垂足为 .
.
(1)求证: 为⊙O的切线;
为⊙O的切线;
(2)若过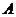 点且与
点且与 平行的直线交
平行的直线交 的延长线于
的延长线于 点,连结
点,连结 .当
.当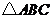 是等边三角形时,求
是等边三角形时,求 的度数.
的度数.
 |
24.(本小题满分9分)
市园林处为了对一段公路进行绿化,计划购买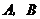 两种风景树共900棵.
两种风景树共900棵.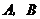 两种树的相关信息如下表:
两种树的相关信息如下表:

单价(元/棵)
成活率
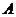
80
92%
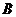
100
98%
若购买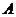 种树
种树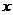 棵,购树所需的总费用为
棵,购树所需的总费用为 元.
元.
(1)求 与
与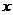 之间的函数关系式;
之间的函数关系式;
(2)若购树的总费用不超过82000元,则购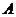 种树不少于多少棵?
种树不少于多少棵?
(3)若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购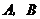 两种树各多少棵?此时最低费用为多少?
两种树各多少棵?此时最低费用为多少?
25.(本小题满分10分)
如图,在 中,
中,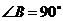 ,
,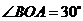 ,
,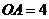 ,将
,将 绕点
绕点 按逆时针方向旋转至
按逆时针方向旋转至 ,
,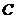 点的坐标为(0,4).
点的坐标为(0,4).
(1)求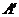 点的坐标;
点的坐标;
(2)求过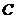 ,
,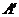 ,
,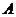 三点的抛物线
三点的抛物线 的解析式;
的解析式;
(3)在(2)中的抛物线上是否存在点 ,使以
,使以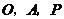 为顶点的三角形是等腰直角三角形?若存在,求出所有点
为顶点的三角形是等腰直角三角形?若存在,求出所有点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

26.(本小题满分12分)
如图,在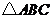 中,
中, ,
,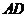 是
是 边上的高,
边上的高, 是
是 边上的一个动点(不与
边上的一个动点(不与 重合),
重合),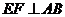 ,
, ,垂足分别为
,垂足分别为 .
.
(1)求证: ;
;
(2)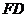 与
与 是否垂直?若垂直,请给出证明;若不垂直,请说明理由;
是否垂直?若垂直,请给出证明;若不垂直,请说明理由;
(3)当 时,
时, 为等腰直角三角形吗?并说明理由.
为等腰直角三角形吗?并说明理由.
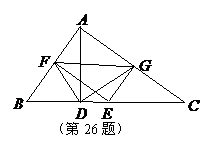 |