2006-2007学年度第二学期期中考试八年级
数学试卷
(考试时间90分钟 满分120分)
友情提示:
本试卷包括第Ⅰ卷、第Ⅱ卷两部分。
第Ⅰ卷为客观题,共30分,答案填在第Ⅱ卷的答题栏内。第Ⅱ卷为主观题,包括两个大题,分别为填空解答题,共90分,答案写在试卷相应位置上。
第Ⅰ卷(选择题共30分)
一、选择题(本大题10个小题,每小题3分,共30分,在每小题给出的四个选项中只有一个是正确的,请把正确答案填在第Ⅱ卷的答题栏内,只填在第Ⅰ卷内不得分.)
1.下列运算中,正确的是( )
(A)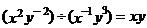 (B)
(B)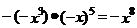
(C)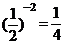 (D)
(D)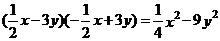
2.计算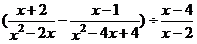 得( )
得( )
(A)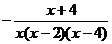 (B)
(B)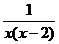 (C)
(C)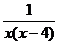 (D)
(D)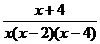
3.若方程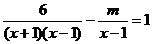 有增根,则它的增根是( )
有增根,则它的增根是( )
(A)0 (B)―1 (C)1 (D)1或―1
4.如图,Rt△ABC中,∠C=90°,AB的垂直平分线交AB于D,交AC于E,且∠EBC=2∠EBA,则∠A等于( )
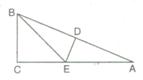
(A)20° (B)22.5° (C)25° (D)27.5°
5.己知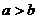 ,且
,且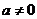 ,
,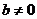 ,
,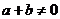 ,则函数
,则函数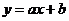 与
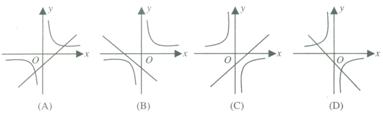
与 在同一坐标系中的图象不可能是( )
在同一坐标系中的图象不可能是( )
6.若用(1),(2),(3),(4)四幅图象分别表示变量之间的关系,将下面的(a),(b),(c),(d)对应的图象排序:
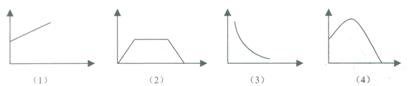
(a)面积为定值的矩形(矩形的相邻两边长的关系)
(b)运动员推出去的铅球(铅球的高度与时间的关系)
(c)一个弹簧不挂重物到逐渐挂重物(弹簧长度与所挂重物质量的关系)
(d)某人从A地到B地后,停留一段时间,然后按原速返回(离开A地的距离与时间的关系),其中正确的顺序是( )
(A)(3)(4)(1)(2) (B)(3)(2)(1)(4) (C)(4)(3)(1)(2) (D)(3)(4)(2)(1)
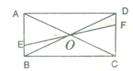
7.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的( )
(A)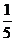 (B)
(B) (C)
(C)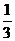 (D)
(D)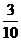
8.如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有( )
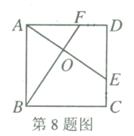
(A)1个 (B)2个 (C)3个 (D)4个
9.已知△ABC.
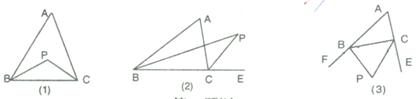
(1)如图1,若点P是∠ABC和∠ACB的角平分线的交点,则∠P=90°+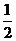 ∠A;
∠A;
(2)如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°―∠A;
(3)如图3,若点P是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°―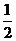 ∠A.
∠A.
上述说法中正确的有( )
(A)0个 (B)1个 (C)2个 (D)3个
10.已知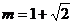 ,
,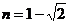 ,且
,且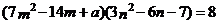 ,则a的值为( )
,则a的值为( )
(A)一5 (B)5 (C)―9 (D)9
第Ⅱ卷 非选择题(共90分)
一、选择题(本大题10个小题,每小题3分,共30分.在每小题给出的四个选项中只有一个是正确的,请把正确答案填在下面的答题栏内.)
11.“平行四边形的对角线互相平分”的逆命题是_________________________________.
12.已知点M(
13.某电视台在黄金时段的2分钟广告时间内,计划插播长度为15秒和30秒的两种广告.15秒的广告每播一次收费0.6万元,30秒的广告每播一次收费1万元.若要求每种广告播放不少于2次,则电视台在播放时最大收益是_________万元.
14.如果记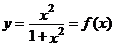 ,并且
,并且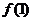 表示
表示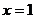 时,
时,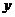 的值,即,
的值,即,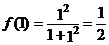 ;
;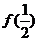 表示
表示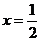 时
时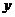 的值,即
的值,即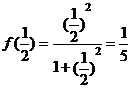 ,那么
,那么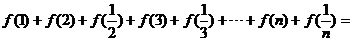 ________.(结果用含
________.(结果用含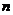 的代数式表示,
的代数式表示,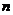 为正整数)
为正整数)
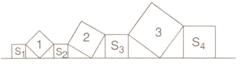
15.在直线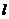 上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积依次为1,2,3,正放置的四个正方形的面积依次为S1,S2,S3,S4,则S1+S2+S3+S4=________.
上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积依次为1,2,3,正放置的四个正方形的面积依次为S1,S2,S3,S4,则S1+S2+S3+S4=________.
16.如图,P是等边三角形ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与点P′之间的距离是_________,∠APB=________.

17.假设一家旅馆一共有30个房间,分别编以1――30三十个号码,现在要在每个房间的钥匙上刻上数字,要求所刻的数字必须使服务员很容易辨认是哪一个房间的钥匙,而使局外人不容易猜到.现在有一种编码的方法是:在每把钥匙上刻上两个数字,左边的一个数字是这把钥匙原来的房间号码除以5所得的余数,而右边的一个数字是这把钥匙原来的房间号码除以7所得的余数.那么刻的数是36的钥匙所对应的原来房间应该是__________号.
18.若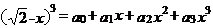 ,则
,则

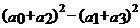 的值为______.
的值为______.
三、解答题(本大题共8个小题,满分66分)
19.(本小题满分8分)如图,已知三角形ABC,其中AB=AC.
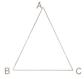
(1)作AB的垂直平分线DE,交AB于D点,AC于E点;连结BE{尺规作图,不写作法,保留作图痕迹)
(2)在(1)的基础上,若AB=8,三角形BCE的周长为14,求BC的长.
20.(本小题满发8分)已知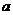 、
、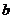 为实数,且
为实数,且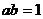 ,设
,设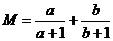 ,
,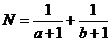 ,试用两种方法比较M、N的大小.
,试用两种方法比较M、N的大小.
材料:一般地,n个相同的因数a相乘:a?a?a…a记为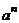 .如
.如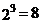 ,此时,3叫做以2为底8的对数,记为log2 8(即log2 8=3).一般地,若
,此时,3叫做以2为底8的对数,记为log2 8(即log2 8=3).一般地,若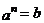 (
(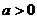 ,且
,且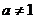 ,
,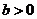 ),则
),则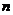 叫做以
叫做以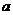 为底
为底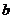 的对数,记为loga b(loga b=n).如
的对数,记为loga b(loga b=n).如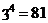 ,则4叫做以3为底81的对数,记为log3 81(即log3 81=4).
,则4叫做以3为底81的对数,记为log3 81(即log3 81=4).
问题:(1)计算以下各对数值
log2 4=_________; log2 16=_________; log2 64=_________.
(2)观察(1)中三数4、16、64之间满足怎样的关系式?log2 4、log2 16、log2 64之间又满足怎样的关系式?
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
logaM+ logaN=___________(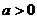 且
且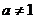 ,
,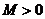 ,
,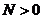 ).
).
根据幂的运算法则: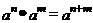 以及对数的含义证明上述结论.
以及对数的含义证明上述结论.
22.(本小题满分8分)
如图1,图2,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.

(1)如图1,当点E在AB边的中点位置时:
①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是______________;
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是________________;
③请证明你的上述两猜想.
(2)如图2,当点E在AB边上的任意位置时,请你在AD边上找到一点N,使得NE=BF,进而猜想此时DE与EF有怎样的数量关系.
23.(本小题满分8分)
观察图①可以得出:直线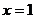 与直线
与直线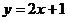 的交点P的坐标(1,3)就是方程组
的交点P的坐标(1,3)就是方程组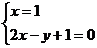 的解,所以这个方程组的解为
的解,所以这个方程组的解为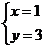 .
.
在直角坐标系中,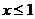 表示一个平面区域,即直线
表示一个平面区域,即直线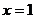 以及它左侧的部分,如图②;
以及它左侧的部分,如图②; 也表示一个平面区域,即直线
也表示一个平面区域,即直线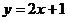 以及它下方的部分,如图③.
以及它下方的部分,如图③.
回答下列问题:
(1)在直角坐标系(图④)中,用作图象的方法求出方程组 的解;
的解;
(2)用阴影表示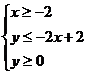 ,所围成的区域.
,所围成的区域.
24.(本小题满分8分)我市对城区沿小康河两岸的部分路段进行亮化工程建设,整个工程拟由甲、乙两个安装公司共同完成.从两个公司的业务资料看到:若两个公司合做,则恰好用12天完成;若甲、乙合做9天后,由甲再单独做5天也恰好完成.如果每天需要支付甲、乙两公司的工程费用分别为1.2万元和0.7万元.
试问:(1)甲、乙两公司单独完成这项工程各需多少天?
(2)要使整个工程费用不超过22.5万元,则乙公司最少应施工多少天?
25.(本大题满分10分)
 第三届南宁国际龙舟赛于
第三届南宁国际龙舟赛于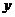 (米)与时间
(米)与时间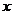 (分钟)的函数图象如图所示,根据函数图象填空和解答问题:
(分钟)的函数图象如图所示,根据函数图象填空和解答问题:

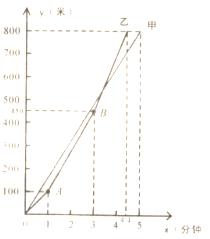
(1)最先到达终点的是___________队,比另一队领先_____________分钟到达;
(2)在比赛过程中,乙队在_______分钟和________分钟时两次加速,图中点A的坐标是____________,点B的坐标是________________.
(3)假设乙队在第一次加速后,始终保持这个速度继续前进,那么甲、乙两队谁先到达终点?请说明理由.
26.(本小题满分8分)探索:在如图(1)至图(3)中,△ABC的面积为a.
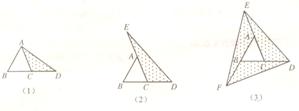
(1)如图(1),延长△ABC的边BC到点D,使CD=BC,连结DA.若△ACD的面积为S1,则S1=____________(用含a的代数式表示);
(2)如图(2),延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则S2=__________(用含a的代数式表示),并写出理由;
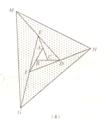
(3)在图(2)的基础上延长AB到点F,使BF=AB,连结FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3=__________(用含a的代数式表示).
发现 像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的__________倍.
应用 去年在面积为