摘要:观察图①可以得出:直线与直线的交点P的坐标(1.3)就是方程组的解.所以这个方程组的解为.
网址:http://m.1010jiajiao.com/timu_id_671176[举报]
如图,直线AB、EF、GH都经过P,直线CD分别截直线EF、GH于点M、N,已知∠APM=90°。∠1=43°,∠2=43°。

(1)观察图形,结合已知条件可以得到以下结论:
①直线GH与直线EF相交于点______;
②直线______⊥______,垂足为______。
(2)问CD与EF是否互相垂直?推理说明你的道理。请你在横线上补充条件或结论,在括号内填写出相应的推理依据。
解:我的结论是__________。
∵∠3=∠________(对顶角相等),
又∵∠2=43°( ) ,
∴∠3=43°(等量代换),
∵∠1=43°(已知),
∴∠1=∠3(等量代换),
∴AB∥CD( ),
∴∠4=∠APM( ),
∵∠APM=________(已知),
∴∠4=________(等量代换),
∴________(垂直的意义)。
查看习题详情和答案>>
①直线GH与直线EF相交于点______;
②直线______⊥______,垂足为______。
(2)问CD与EF是否互相垂直?推理说明你的道理。请你在横线上补充条件或结论,在括号内填写出相应的推理依据。
解:我的结论是__________。
∵∠3=∠________(对顶角相等),
又∵∠2=43°( ) ,
∴∠3=43°(等量代换),
∵∠1=43°(已知),
∴∠1=∠3(等量代换),
∴AB∥CD( ),
∴∠4=∠APM( ),
∵∠APM=________(已知),
∴∠4=________(等量代换),
∴________(垂直的意义)。
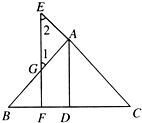 23、已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
23、已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.求证:AD平分∠BAC,填写分析和证明中的空白.
分析:要证明AD平分∠BAC,只要证明
∠BAD
=∠CAD
,而已知∠1=∠2,所以应联想这两个角分别和∠1、∠2的关系,由已知BC的两条垂线可推出
EF
∥AD
,这时再观察这两对角的关系已不难得到结论.证明:∵AD⊥BC,EF⊥BC(已知)
∴
EF
∥AD
(在同一平面内,垂直与同一直线的两直线平行
)∴
∠1
=∠BAD
(两直线平行,内错角相等),∠2
=∠CAD
(两直线平行,同位角相等)∵
∠1=∠2
(已知)∴
∠BAD=∠CAD
,即AD平分∠BAC(角平分线的定义
)
我们知道,在数轴上,x=1表示一个点,而在平面直角坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象,它也是一条直线,如图1.
观察图1可以得出:直线x=1与直线y=2x+1的交点P的坐标(1,3)就是
方程组
的解,所以这个方程组的解为
.
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图②;y≤2x+1也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图3;
那么,
所围成的区域就是图4中的阴影部分.

回答下列问题:
(1)在下面的直角坐标系中,用作图象的方法求出方程组
的解;
(2)在右面的直角坐标系中用阴影表示,
所围成的区域.
查看习题详情和答案>>
观察图1可以得出:直线x=1与直线y=2x+1的交点P的坐标(1,3)就是
方程组
|
|
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图②;y≤2x+1也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图3;
那么,
|

回答下列问题:
(1)在下面的直角坐标系中,用作图象的方法求出方程组
|
(2)在右面的直角坐标系中用阴影表示,
|
我们知道,在数轴上,x=1表示一个点,而在平面直角坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象,它也是一条直线,如图1.
观察图1可以得出:直线x=1与直线y=2x+1的交点P的坐标(1,3)就是
方程组 的解,所以这个方程组的解为
的解,所以这个方程组的解为 .
.
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图②;y≤2x+1也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图3;
那么,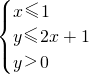 所围成的区域就是图4中的阴影部分.
所围成的区域就是图4中的阴影部分.

回答下列问题:
(1)在下面的直角坐标系中,用作图象的方法求出方程组 的解;
的解;
(2)在右面的直角坐标系中用阴影表示,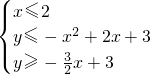 所围成的区域.
所围成的区域.
查看习题详情和答案>>
我们知道,在数轴上,x=1表示一个点,而在平面直角坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象,它也是一条直线,如图1.
观察图1可以得出:直线x=1与直线y=2x+1的交点P的坐标(1,3)就是
方程组
的解,所以这个方程组的解为
.
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图②;y≤2x+1也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图3;
那么,
所围成的区域就是图4中的阴影部分.

回答下列问题:
(1)在下面的直角坐标系中,用作图象的方法求出方程组
的解;
(2)在右面的直角坐标系中用阴影表示,
所围成的区域.
查看习题详情和答案>>
观察图1可以得出:直线x=1与直线y=2x+1的交点P的坐标(1,3)就是
方程组
|
|
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图②;y≤2x+1也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图3;
那么,
|

回答下列问题:
(1)在下面的直角坐标系中,用作图象的方法求出方程组
|
(2)在右面的直角坐标系中用阴影表示,
|