2005年临沂市高中阶段学校招生考试(非课改实验区用)
第Ⅰ卷
一、选择题(本题共14小题,每小题3分,共42分)在每小题所给的四个选项中,只有一项是符合要求的。
1、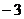 的绝对值是
的绝对值是
A、3 B、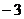 C、
C、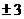 D、
D、
2、2004年临沂市的国民生产总值为1012亿元,用科学记数法表示正确的是
A、1012×108元
B、1.012×1011元
C、1.0×1011元
D、1.012×1012元
3、下我各式计算正确的是
A、(a5)2=a7 B、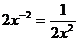
C、3a2•2a3=6a6 D、a8÷a2=a6
4、如图,将两根钢条AA’、BB’的中点O连在一起,使AA’、BB’可以绕着点O自由转动,就做成了一个测量工件,则A’B’的长等于内槽宽AB,那么判定△OAB≌△OAB的理由是
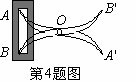
A、边角边。B、角边角。C、边边边。D、角角边。
5、两圆半径分别为8和3,外公切线长为9,则两圆的位置关系是
A、内切 B、相交
C、外切 D、外离
6、化简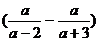 •
• 的结果是
的结果是
A、1 B、5
C、2a+1 D、2a+5
7、如图,顺次连结圆内接矩形各边的中点,得到菱形ABCD,若BD=10,DF=4,则菱形ABCD的边长为
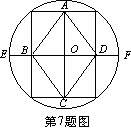
A、 B、
B、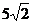 C、6 D、9
C、6 D、9
8、把45ab2-20a因式分解的结果是
A、5ab(9b-4) B、5a(9b2-4)
C、5a(3b-2)2 D、5a(3b+2)(3b-2)
9、凸n边形的内角中,锐角的个数最多有
A、1个 B、2个 C、3个 D、4个
10、如图,已知点A的坐标为(1,0),点B在直线y=-x上运动,当线段AB最短时,点B的坐标为
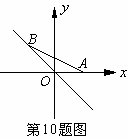
A、(0,0)
B、(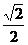 ,
,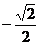 )
)
C、( ,
,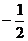 )
D、(
)
D、(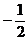 ,
,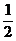 )
)
11、解分式方程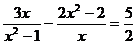 时,设
时,设 ,则原方程可化为
,则原方程可化为
A、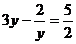 B、
B、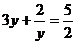
C、 D、
D、
12、等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为
A、60° B、120°
C、60°或150° D、60°或120°
13、用配方法将二次函数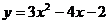 写成形如
写成形如 的形式,则m、n的值分别是
的形式,则m、n的值分别是
A、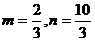 B、
B、
C、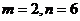 D、
D、
14、已知△ABC,
⑴如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°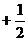 ∠A;
∠A;
⑵如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;
⑶如图3,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°- ∠A。
∠A。

上述说法下确的个数是
A、0个 B、1个 C、2个 D、3个
第Ⅱ卷
二、填空题(本大题共5小题,每小题3分,共15分)把答案填在题中横线上。
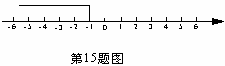
15、关于x的不等式3x?2a≤?2的解集如图所示,则a的值是 。
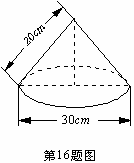
16、如图是小芳学习时使用的圆锥形台灯灯罩的示意图,则围成这个灯罩的铁皮的面积为 cm2(不考虑接缝等因素,计算结果用π表示)。
17、若圆周角α所对弦长为sinα,则此圆的半径r为 。
18、请写出一个一元二次方程,要求二次项系数不为1,且其两根互为倒数
19、判断一个整数能否被7整除,只需看去掉一节尾(这个数的末位数字)后所得到的数与此一节尾的5倍的和能否被7整除,如果这个和能被7整除,则原数就能被7整除,如126,去掉6后得12,12+6×5=42,42能被7整除,则126能被7整除,类似地,还可通过看去掉该数的一节尾后与此一节尾的n倍的差能否被7整除来判断,则n= (n是整数,且1≤n<7)。
三、解答题
20、(本小题满分6分)
为了了解家庭日常生活消费情况,小亮记录了他家一年中7周的日常生活消费费用,数据如下(单位:元):
230 195 180 250 270 455 170
请你用统计初步的知识,计算小亮家平均每年(每年按52周计算)的日常生活消费总费用。
21、(本小题满分7分)
李明家和陈刚家都从甲、乙两供水点购买同样的一种桶装矿泉水,李明家第一季度从甲、乙两供水点分别购买了10桶和6桶,共花费51元;陈刚家第一季度从甲、乙两供水点分别购买了8桶和12桶。且在乙供水点比在甲供水点多花18元钱。若只考虑价格因素,通过计算说明到哪家供水点购买这种桶装矿泉水更便宜一些?
22、(本小题满分8分)
如图,已知AD和BC交于点O,且△OAB和△OCD均为等边三角形,以OD和OB为边作平行四边形ODEB,连结AC、AE和CE,CE和AD相交于点F。求证:△ACE为等边三角形。
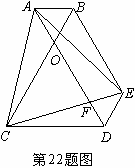
四、
23、(本小题满分9分)
如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BC的延长线于点P,交AD的延长线于点E,若AD=5,AB=6,BC=9。
⑴求DC的长;
⑵求证:四边形ABCE是平行四边形。

24、(本小题满分10分)
某厂从2001年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具休数据如下表:
年 度
2001
2002
2003
2004
投入技改资金x(万元)
2.5
3
4
4.5
产品成本y(万元/件)
7.2
6
4.5
4
⑴请你认真分析表中数据,从你所学习过的一次函数、二次函数和反比例函数中确定哪种函数能表示其变化规律,说明确定是这种函数而不是其它函数的理由,并求出它的解析式;
⑵按照这种变化规律,若2005年已投入技改资金5万元。
①预计生产成本每件比2004年降低多少万元?
②如果打算在2005年把每件产品成本降低到3.2万元,则还需投入技改资金多少万元?(结果精确到0.01万元)?
五、相信自己,加油呀!
25、(本小题满分10分)
△ABC中,BC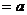 ,AC
,AC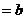 ,AB
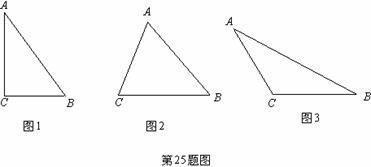
,AB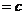 ,若∠C=90°,如图1,根据勾股定理,则
,若∠C=90°,如图1,根据勾股定理,则 ,若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想
,若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想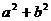 与
与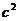 的关系,并证明你的结论。
的关系,并证明你的结论。
26、(本小题满分13分)
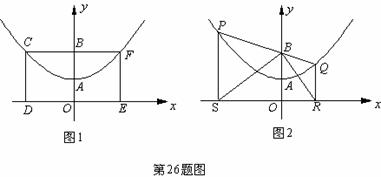
如图1,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,D、E在x轴上,CF交y轴于点B(2,0),且其面积为8。
⑴ 求此抛物线的解析式;
⑵ 如图2,若P点为抛物线上不同于A的一点,连结PB并延长交抛物线于点Q,过点P、Q分别作x轴的垂线,垂足分别为S、R。
①求证:PB=PS;
②判断△SBR的形状;
③试探索在线段SR上是否存在点M,使得以点A、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似,若存在,请找出M点的位置;若不存在,请说明理由。