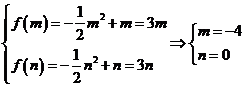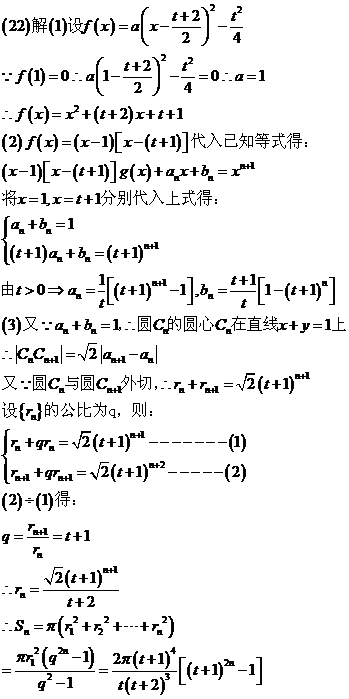安徽省皖北十三所省示范高中十二月高三联考数学试卷(理科)
一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项是符合题目要求的)
1.设集合 ,若
,若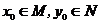 ,则
,则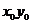 与集合
与集合 的关系是
的关系是
A.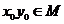 B.
B. C.
C. D.无法确定
D.无法确定
2.已知 是定义在R上的奇函数且满足
是定义在R上的奇函数且满足 ,当
,当 时,
时, ,则使
,则使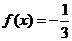 的值等于
的值等于
A.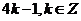 B.
B. C.
C.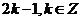 D.
D.
3.已知图甲中的图像对应的函数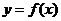 ,则图乙中的图像对应的函数在下列给出的四式中只可能是
,则图乙中的图像对应的函数在下列给出的四式中只可能是
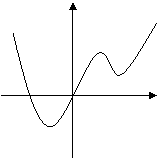
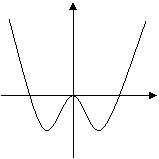
甲 乙
A.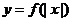 B.
B.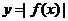 C.
C.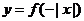 D.
D.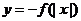
4.已知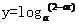 在[0,1]上是x的减函数,则a的取值范围是
在[0,1]上是x的减函数,则a的取值范围是
A.(0,1) B.(1,2) C.(0,2) D.[2,+∞)
5.已知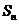 是等差数列
是等差数列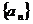 的前n项和,若
的前n项和,若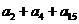 是一个确定的常数,则数列
是一个确定的常数,则数列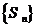 中是常数的项为
中是常数的项为
A.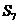 B.
B.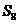 C.
C.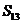 D.
D.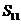
6.函数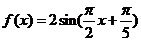 ,若对任意
,若对任意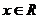 ,都有
,都有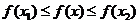 成立,则
成立,则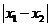 的最小值为
的最小值为
A.4 B.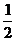
7.如图,为一半径为3米的水轮,水轮圆心O距离水面2米,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y(米)与时间x(秒)满足函数关系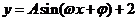 ,则
,则
 A.
A.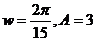
B.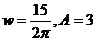
C.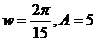
D.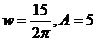
8.向量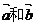 的夹角平分线上的单位向量是
的夹角平分线上的单位向量是
A.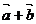 B.
B.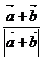 C.
C. 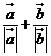 D.
D.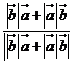
9.对于-1≤a≤1,不等式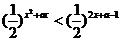 恒成立的x的取值范围是
恒成立的x的取值范围是
A.x<0或x>2 B.0<x<2 C.x<1或x>3 D.-1<x<1
10.已知三个不等式①x 2-4 x +3<0;②x 2-6 x +8<0;③2 x 2-9 x +m<0,要使同时满足①和②的所有x的值都满足③,则实数m的取值范围为
A.m>9 B.m =9 C.m≤9 D.0<m≤9
11.若点(5,b)在两条平行直线6x-8y+1=0与3x-4y+5=0之间,则整数b的值为
A.-4 B.4 C.-5 D.5
12.圆(x-3)2+(y+5)2=r2上有且仅有两点到直线4x-3y-2=0的距离为1,则半径r的取值范围是
A.0<r<4 B.r>4 C.4<r<6 D.r>6
二、填空:(本大题共4小题,每小题4分,共16分,请将答案写在横线上)
13.函数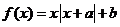 是奇函数的主要条件是
。
是奇函数的主要条件是
。
14.若存在常数p>0,使得函数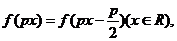 则
则 的最小正周期为 。
的最小正周期为 。
15.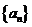 是公比为q的等比数列,
是公比为q的等比数列,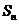 是它的前n项和,若
是它的前n项和,若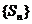 是等差数列,则q= 。
是等差数列,则q= 。
16.关于x的函数f(x)=sin(x+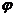 )有以下命题:
)有以下命题:
①对任意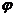 ,f(x)都是非奇非偶函数;
,f(x)都是非奇非偶函数;
②不存在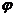 ,使f(x)既是奇函数,又是偶函数;
,使f(x)既是奇函数,又是偶函数;
③存在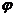 ,使f(x)是奇函数;
,使f(x)是奇函数;
④对任意的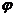 ,f(x)都不是偶函数。
,f(x)都不是偶函数。
其中一个假命题的序号是
因为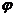 =
时,该命题结论不成立。
=
时,该命题结论不成立。
三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)已知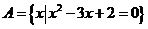 ,
,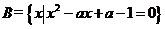 ,
,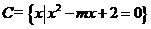 且
且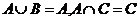 ,求实数a及m值。
,求实数a及m值。
18.(本小题满分12分)已知直线y=x+a与y=x2有两个交点A、B
(1)求 ;(2)证明:
;(2)证明: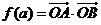 ,求
,求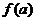 的最小值。
的最小值。
19.(本小题满分12分)已知函数 =2
=2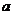
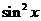 -2
-2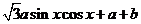 定义域为[
定义域为[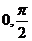 ],值域为[-5,1],求常数a、b值。
],值域为[-5,1],求常数a、b值。
20.(本小题满分12分)已知数列 的前n项和为
的前n项和为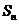 且满足
且满足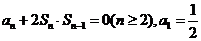
(1)求证:数列 为等差数列;
为等差数列;
(2)求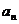 的表达式;
的表达式;
(3)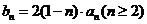 时,求证:
时,求证: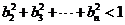 。
。
21.(本小题满分12分)已知二次函数f(x)=ax2+bx+c满足如下条件:①图象过原点;②f(-x+2002)=f(x-2002);③方程f(x)=x有重根。
(1)求f(x)的解析式。
(2)是否存在实数m, n(m<n)使f(x)的定域和值域分别为[m, n]和[3 m,3n]若存在,求出m, n的值,若不存在,说明重点。
22.(本小题满分14分)已知二次函数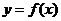 在
在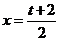 处取得最小值
处取得最小值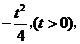 且
且
(1)求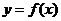 的表达式;
的表达式;
(2)若任意实数x都满足 (
(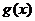 为多项式,
为多项式,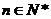 ),试用t表示
),试用t表示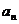 和
和 。
。
(3)设圆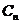 的方程为
的方程为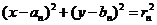 ,圆
,圆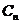 与
与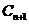 外切(n=1、2…)
外切(n=1、2…)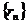 是各项都是正数的等比数列,记
是各项都是正数的等比数列,记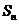 为前n个圆的面积的和,求
为前n个圆的面积的和,求 。
。
数学答案(理科)
1.A 2.A 3.C 4.B 5.C 6.B 7.A 8.D 9.A 10.C
11.B 12.C
13. 14.
14. 15.q=1
15.q=1
16.(1) ;或者(1)
;或者(1) ;或者(4)
;或者(4) 三组项任一组都给分。.
三组项任一组都给分。.
17.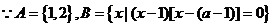 及
及
∴ (此时
(此时 )或
)或 (此时
(此时 为其二重根。
为其二重根。
由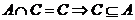
当 时,显然不成立,从而
时,显然不成立,从而 ;
;
当 时,
时,
当 ,由
,由
综上可得,
18.
(1)设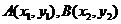 ,联立
,联立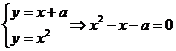 ①
①
∴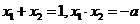 ,∴
,∴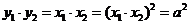
∴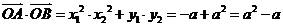
(2)由①式的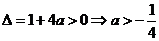
∴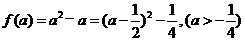 ,
,
∴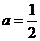 时,
时,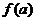 有最小值
有最小值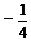
19.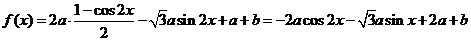
∴
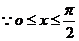 ,∴
,∴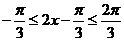 ,∴
,∴
1°, 时,
时, 不合题意;
不合题意;
2°,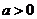 时,
时,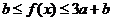 ,则
,则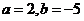
3°, 时,
时,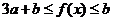 ,则
,则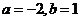
综上,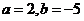 或
或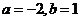
20.
(1)证明: ,∴
,∴
∴
又 ,∴
,∴ 是以2为首项,2为公差的等差数列
是以2为首项,2为公差的等差数列
(2)由(1)得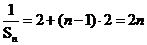 ,∴
,∴
当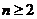 时,
时,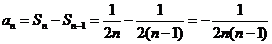
当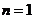 时,
时,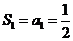
∴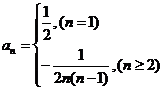
(3)由(2)知,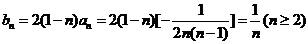
∴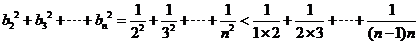
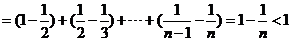
21.
(1)∵图像过原点,∴
∵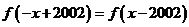 ,∴
,∴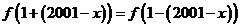
∴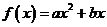 的对称轴为
的对称轴为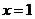 ,即
,即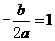 ①
①
又∵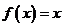 ,即方程
,即方程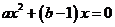 ,∴
,∴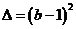 ,
,
∴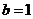 代入①
代入①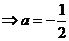
∴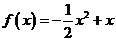
(2) ,∴
,∴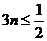 ,∴
,∴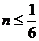
∴在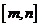 上
上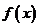 为增函数,
为增函数,
∴有